Fundamentals of Zener Diodes

Introduction to Special Purpose Diodes

Rectifier Diodes:
- Commonly used for converting AC voltage to DC in power supplies.
Beyond Rectification:
- Diodes serve in various applications beyond rectification.
Zener Diodes:
- Optimized for breakdown properties.
- Essential for voltage regulation in circuits.
Other Diodes Covered:
- Optoelectronic Diodes (e.g., LEDs)
- Schottky Diodes (known for low forward voltage drop)
- Varactor Diodes (used for variable capacitance)
- Additional special-purpose diodes for specific applications.

SECTION 01

The Zener Diode

Operation:
- Unlike small-signal and rectifier diodes, Zener diodes are designed to operate in the breakdown region.
- Backbone of voltage regulators, maintaining a nearly constant load voltage despite fluctuations.
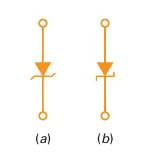
Schematic Symbol:
- Two variations of Zener diode symbols resemble a “z” for "Zener."
Breakdown Voltages:
- Vary from 2V to over 1000V, depending on doping levels.

SECTION 02

I-V Characteristics of Zener Diode

Operating Regions:
1. Forward Region:
  - Conducts at \(\sim0.7~\mathrm{V}\), like a regular silicon diode.
2. Leakage Region:
  - Small reverse current between zero and breakdown.
3. Breakdown Region:
  - Sharp knee followed by a near-vertical increase in current.
  - Voltage stays approximately constant \((V_Z)\) in the breakdown region.
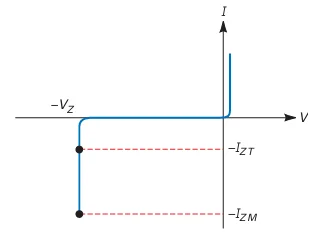
Safe Operation:
- Maximum reverse current: \(I_{ZM}\).
- Exceeding \(I_{ZM}\) leads to diode destruction.
- A current-limiting resistor is essential to protect the diode.

SECTION 03

Zener Resistance

Third Approximation of a Diode:
- Forward voltage = Knee voltage + Voltage across bulk resistance
- Reverse voltage = Breakdown voltage + Voltage across bulk (Zener) resistance
Zener Resistance:
- Defined as the inverse slope of the I-V curve in the breakdown region.
- More vertical breakdown region = smaller Zener resistance
Effect on Reverse Current:
- Increase in reverse current leads to a slight increase in reverse voltage.
- Typically, this voltage increase is only a few tenths of a volt.

Design Considerations:
- Zener resistance matters in design but is often ignored in troubleshooting or preliminary analysis.
Visual Representation:
- Fig. shows typical Zener diodes.

SECTION 04

Zener Regulator

Constant Output Voltage:
- Zener diode maintains a constant output voltage even as current changes.
- Requires reverse bias for normal operation.
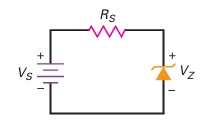
Operating Conditions:
- Source voltage (\(V_s\)) must be greater than Zener breakdown voltage (\(V_Z\)).
- A series resistor (\(R_s\)) is used to limit current and prevent burnout.

Voltage Measurement :
- Measure voltage across \(R_s\) by taking readings at each end with respect to ground.
- Subtract voltages to find the voltage across the series resistor.
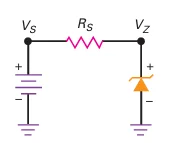
Zener Voltage Regulator :
- A Zener regulator provides a DC output voltage that is less than the power supply output.
- Commonly used for voltage regulation in circuits.

SECTION 05

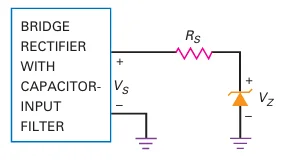
Zener Regulator – Current Calculation

Current through Series Resistor:
- Voltage across the series resistor (\(R_s\)) = Source voltage \((V_S)\) - Zener voltage \((V_Z)\).
- Current through the resistor:
- \(I_s\) is equal to the Zener current since the circuit is in series.
- Important: \(I_s\) must be less than \(I_{ZM}\) to prevent damage.

\[I_S = \frac{V_S - V_Z}{R_S}\]

SECTION 06

Ideal Zener Diode Approximation

Ideal Zener Diode:
- For troubleshooting and analysis, the breakdown region can be approximated as vertical.
- Voltage is constant even with varying current (ignoring Zener resistance).
Circuit Simplification:
- A Zener diode in the breakdown region acts like a constant voltage source \((V_Z)\) .
- This simplifies analysis as you can mentally replace the Zener diode with a battery of voltage \(V_Z\).

SECTION 07

Problem-1

The breakdown voltage of the zener diode shown in the Fig. is 10 V. What are the minimum and maximum zener currents?
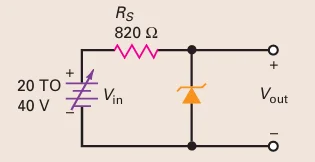
Applied voltage \(20-40~\mathrm{V}\) (vary)
Zener diode replace with a battery of \(10~\mathrm{V} \Rightarrow\) output voltage is \(10~\mathrm{V}\) (fixed)

\[\begin{aligned} \text{Min. current}~I_{S}&=\frac{(20-10)~ \mathrm{V}}{820 \Omega}=12.2 \mathrm{mA} \\ \text{Max. current}~I_{S}&=\frac{(40-10)~ \mathrm{V}}{820 \Omega}=36.6 \mathrm{mA} \end{aligned}\]

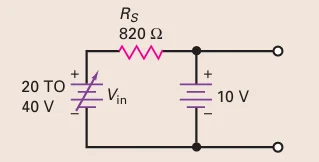
Output Voltage Stability: Held constant at 10 V.
Source Voltage Variation: Changes from 20 V to 40 V.
Zener Diode Behavior:
- Increased source voltage leads to more Zener current.
- Output voltage remains rock-solid at 10 V.

Conclusion: Zener diode ensures stable output voltage despite changes in input voltage.

SECTION 08

Loaded Zener Regulator

Operation:
- Zener diode holds load voltage constant in the breakdown region.
- Load voltage \((V_L)\) stays fixed at the Zener voltage \((V_Z)\) despite changes in source voltage or load resistance.
Voltage Divider & Thevenin Voltage:
- Thevenin voltage (\(V_{TH}\)) facing the diode:
- Breakdown occurs only if \(V_{TH} > V_Z\).

\[V_{TH} = \frac{R_{L}}{R_{S} + R_{L}}V_{S}\]

SECTION 09

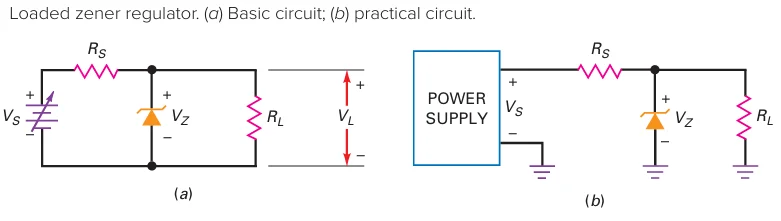
Current Calculations in Loaded Zener Regulator

\[I_S = \frac{V_S - V_Z}{R_S}\]
\((I_S)\)Series Current
\(I_S\) remains the same whether or not the load resistor is connected.
Load Voltage \((V_L)\):
- Ideally, \(V_L = V_Z\) because the load resistor is in parallel with the Zener diode.
\[I_L = \frac{V_L}{R_L}\]
\((IL)\)Load Current

SECTION 10

Zener Current Calculation

\[I_S = I_Z + I_L\]
\((I_S)\)Total Current
The sum of Zener current and load current equals the series current (Kirchhoff’s Current Law).
\[I_Z = I_S - I_L\]
\((I_Z)\)Zener Current
\(I_Z\) no longer equals \(I_S\) as in an unloaded regulator; it’s reduced by the load current.

SECTION 11

Summary of Loaded Zener Regulator Analysis

\[I_S = \frac{V_S - V_Z}{R_S}\]
\((I_S)\)Calculate Series Current
\[V_L = V_Z\]
\((V_L)\)Determine Load Voltage
\[I_L = \frac{V_L}{R_L}\]
\((I_L)\)Calculate Load Current
\[I_Z = I_S - I_L\]
\((I_Z)\)Find Zener Current