Demonstrative Video
Carrier Concentration in Intrinsic Semiconductors
- \[\begin{aligned} & \text{Concentration of free electrons}~ (e) + \text{free holes}~ (p) \end{aligned}\]Conductivity of a semiconductor:
- \[\begin{aligned} N(E) & = \gamma \cdot \left(E-E_c\right)^{1/2} \end{aligned}\]\(E_c\)The density of states is given by
- \[\begin{aligned} f(E)& = \dfrac{1}{1+e^{(E-E_F)/kT}} \end{aligned}\]\(E_F\)The Fermi Dirac probability function
- \[\begin{aligned} n &=\int_{E_c}^{\infty} N(E) f(E) \mathrm{d} E \\ f(E) &=\mathrm{e}^{-\left(E-E_F\right) / k T} \quad \text{for}~ E \geq E_C, ~E-E_F>>k T \\ n &=\int_{E_c}^{\infty} \gamma\left(E-E_C\right)^{\frac{1}{2}} \mathrm{e}^{-\left(E - E_F\right) / k T} \mathrm{~d} E \\ n &=N_C \cdot \mathrm{e}^{-\left(E_c-E_F\right) / k T} \\ N_C &=2\left(\frac{2 \pi m_n k T}{h^2}\right)^{3 / 2}\left(1.60 \times 10^{-19}\right)^{3 / 2} \end{aligned}\]\(m_n\)Concentration of electrons in conduction band
- \[\begin{aligned} N(E) & = \gamma \cdot (E_v-E)^{1/2} \end{aligned}\]is the maximum valence band energy, the density of states is If
- \[\begin{aligned} 1-f(E) &=\frac{\mathrm{e}^{\left(E-E_F\right) / k T}}{1+\mathrm{e}^{\left(E-E_F\right) / k T}}=\mathrm{e}^{-\left(E_F-E\right) / k T} \quad E_F-E>>k \text { for } E \leq E_V \\ p &=\int_{-\infty}^{E_v} \gamma\left(E_V-E\right)^{1 / 2} \mathrm{e}^{-\left(E_F-E\right) / k T} \mathrm{~d} E \\ p &=N_v \cdot \mathrm{e}^{\left(E_F-E_v\right) / k T} \\ N_v &=2\left(\frac{2 \pi m_p k T}{h^2}\right)^{3 / 2}\left(1.60 \times 10^{-19}\right)^{3 / 2} \end{aligned}\]\(m_p\)For holes calculation:
- \[\begin{aligned} n_i &=p_i \\ N_C \cdot \mathrm{e}^{-\left(E_c-E_F\right) / k T} &=N_V \cdot \mathrm{e}^{-\left(E_F-E_v\right) / k T} \\ \text{Taking logarithmic}~ \operatorname{ln} \frac{N_C}{N_V} &=\frac{E_C+E_V-2 E_F}{k T} \\ E_F &=\frac{E_C+E_V}{2}-\frac{k T}{2} \ln \frac{N_C}{N_V} \\ N_C &=N_V \quad (\text{considering same effective masses }) \\ E_F &=\frac{E_C+E_V}{2} \end{aligned}\]From the equation, at the centre of the forbidden energy band, Fermi level is presentFermi level of an intrinsic semiconductor:
Fermi level of an extrinsic semiconductor:
\[\begin{aligned}
{\color{teal}{\textbf{N-type}}} & \\
E_F& =E_C+k T \ln \frac{N_C}{N_D} \\
N_D&=N_C \cdot \mathrm{e}^{-\left(E_C-E_F\right) / k T} \\
\end{aligned}\]
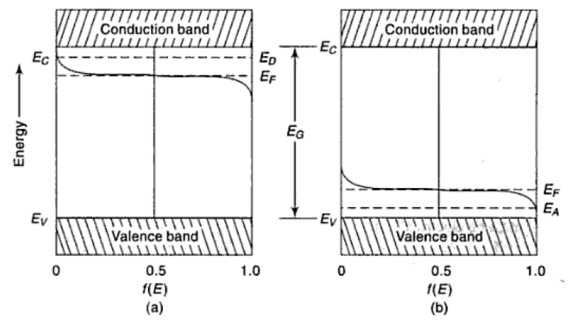
As temperature \(\uparrow\), \(E_F\) moves towards the middle of the forbidden energy gap
Problem-1
In an N-type semiconductor, the Fermi level is 0.3 eV below the conduction level at a room temperature of \(300^\circ\)K. If the temperature is increased to \(360^\circ\)K, determine the new position of the Fermi level?
\[\begin{aligned}
\text{For N-type material:}~E_F & = E_C -
kT\operatorname{ln}\dfrac{N_C}{N_D} \\
\Rightarrow ~ \left(E_C - E_F\right) & = kT
\operatorname{ln}\dfrac{N_C}{N_D}\\
\Rightarrow~0.3 & = 300k\operatorname{ln}\dfrac{N_C}{N_D} \qquad
(1)\\
\text{Also}~E_C-E_{F1} & = 360k\operatorname{ln}\dfrac{N_C}{N_D}
\qquad (2)\\
\Rightarrow~\dfrac{E_C-E_{F1}}{0.3} & = \dfrac{360}{300} \\
\Rightarrow~E_C-E_{F1} & = \dfrac{360}{300}\times 0.3 =
0.36~\mathrm{eV}~(\text{Ans})
\end{aligned}\]
Problem-2
In a p-type semiconductor, the Fermi level is 0.3 eV above the valence band at \(300^{\circ}\)K. Determine the new position of the Fermi level for (a) \(300^{\circ}\)K and (b) \(400^{\circ}\)K ?
\[\begin{aligned}
E_F & = E_v +kT \operatorname{ln} \dfrac{N_V}{N_A}
\Rightarrow (E_F-E_V) = kT \operatorname{ln}\dfrac{N_V}{N_A} \\
T=300^{\circ}K \Rightarrow 0.3 & =
300k\operatorname{ln}\dfrac{N_V}{N_A} \qquad (1) \\
T=350^{\circ}K \Rightarrow (E_{F1}-E_V) & =
350k\operatorname{ln}\dfrac{N_V}{N_A} \qquad (2) \\
\text{From (1) and (2)} & \\
(E_{F1}-E_V) & = \dfrac{350}{300}\times 0.3=0.35~\mathrm{eV}\\
T=400^{\circ}K \Rightarrow (E_{F2}-E_V) & =
400k\operatorname{ln}\dfrac{N_V}{N_A} \qquad (3) \\
\Rightarrow~ \dfrac{E_{F2}-E_V}{0.3} & = \dfrac{400}{300}
\Rightarrow~ (E_{F2}-E_V) = \dfrac{400}{300}\times 0.3 =
0.4~\mathrm{eV}
\end{aligned}\]