Field-effect transistor (FET)s

Introduction

  • Transistors are essential semiconductor devices.

  • Two major types:

    • Bipolar Junction Transistor (BJT)

    • Field-Effect Transistor (FET)

  • BJTs use both electrons and holes (bipolar)

  • FETs use only one type of charge carrier (unipolar).

What is a Field-Effect Transistor (FET)?

  • A voltage-controlled semiconductor device.

  • Controls current flow using an electric field.

  • Two main types:

    • Junction Field-Effect Transistor (JFET)

    • Metal-Oxide Semiconductor Field-Effect Transistor (MOSFET)

BJT vs. FET

Feature BJT FET
Charge Carriers Electrons & Holes (Bipolar) Electrons or Holes (Unipolar)
Control Mechanism Current-Controlled Voltage-Controlled
Input Impedance Low High
Switching Speed Slower Faster
Preferred Applications Amplifiers Switching & High Impedance Circuits

Junction Field-Effect Transistor (JFET)

  • Consists of three terminals: Gate, Source, and Drain.

  • Operates with reverse-biased pn junction to control current in a channel.

  • Two types based on channel structure:

    • N-channel JFET: Current flows through an n-type channel.

    • P-channel JFET: Current flows through a p-type channel.

  • High input impedance, making it useful in high-impedance amplifiers.

image

Basic Operation of JFET

  • Reverse-biased gate-source junction controls current flow.

  • \(V_{DD}\) provides drain-to-source voltage, allowing current flow from drain to source.

  • \(V_{GG}\) sets reverse-bias voltage, producing a depletion region along the pn junction.

  • The depletion region controls channel width and resistance.

  • Wider depletion region towards the drain end due to greater reverse-bias voltage.

image

JFET Characteristics and Parameters

  • Voltage-Controlled Device: JFET operates as a voltage-controlled, constant-current device.

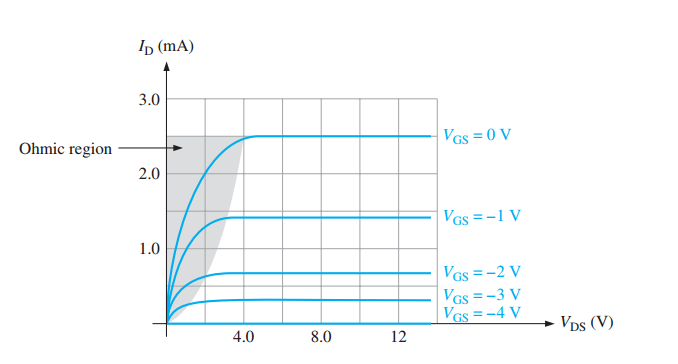
  • Drain Characteristic Curve:

    • \(I_D\) increases with \(V_{DS}\) initially (Ohmic region) but becomes constant in the active region.

    • Pinch-off voltage (\(V_p\)) is where \(I_D\) becomes constant.

image

  • Breakdown Region:

    • Occurs when \(I_D\) increases rapidly beyond safe limits.

    • JFET must be operated below breakdown voltage.

  • \(V_{GS}\) Controls \(I_D\):

    • Increasing negative \(V_{GS}\) reduces \(I_D\) due to narrowing of the channel.

    • The cutoff voltage (\(V_{GS}\text{(off)}\)) is where \(I_D\) is approximately zero.

    • For an n-channel JFET, the more negative \(V_{GS}\) is, the smaller \(I_D\) becomes.

    • \(V_{GS}\)(off) and \(V_p\) are equal in magnitude but opposite in sign.

image

JFET Universal Transfer Characteristic

  • Transfer characteristic curve: \(V_{GS}\) and \(I_{D}\) relationship.

  • Also known as the transconductance curve.

  • Key characteristics:

    • \(I_{D} = 0\) when \(V_{GS} = V_{GS(off)}\)

    • \(I_{D} = I_{DSS}\) at \(V_{GS} = 0\)

    • \(I_{D}\) follows a square-law relationship:

    • \[I_{D} \approx I_{DSS} \left( 1 - \frac{V_{GS}}{V_{GS(off)}} \right)^2\]

  • \(I_{D}\) can be determined for any \(V_{GS}\) if \(V_{GS(off)}\) and \(I_{DSS}\) are given.

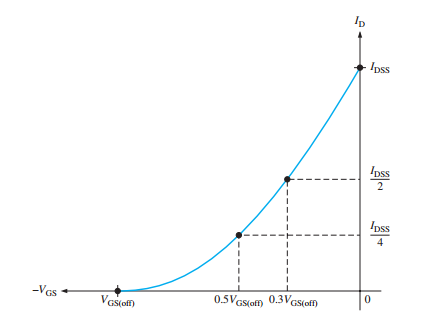
image

  • An example of how the transfer characteristic curve (blue) of an n-channel JFET is developed from the JFET drain characteristic curves (green).

image

JFET Forward Transconductance

  • \[\begin{aligned} g_m & = \frac{\Delta I_D}{\Delta V_{GS}} \\ g_m & = g_{m0} \left(1 - \frac{V_{GS}}{V_{GS(off)}} \right)\\ g_{m0} &\Rightarrow~ \text{transconductance at}~ V_{GS} = 0 \end{aligned}\]
    \(\Delta V_{GS}\)\(\Delta I_D\)Forward Transconductance (g\(_m\)):
  • \[g_{m0} = \frac{2 I_{DSS}}{|V_{GS(off)}|}\]
    is unknown, it can be estimated as: When
image

  • JFET has high input resistance (\(R_{IN}\)) due to reverse-biased gate-source junction.

    \[R_{IN} = \left| \frac{V_{GS}}{I_{GSS}} \right|\]

  • Input Capacitance (C\(_{iss}\)): Results from the reverse-biased pn junction.

  • AC Drain-to-Source Resistance (r\(_{ds}'\)): Resistance in the active region where \(I_D\) remains constant over a range of \(V_{DS}\).

    \[r_{ds}' = \frac{\Delta V_{DS}}{\Delta I_D}\]

  • Often specified in terms of output conductance \(g_{os}\).

JFET Biasing

  • The purpose of biasing is to set a proper Q-point.

  • Three types of biasing in the active region:

    • Self-bias

    • Voltage-divider bias

    • Current-source bias

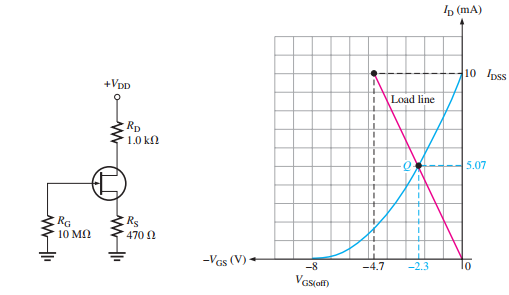
Self-Biasing

  • Ensures gate-source junction is reverse-biased.

    \[\begin{aligned} V_{GS} &= -I_D R_S \Leftarrow \text{n-channel JFET}\\ V_{GS} &= +I_D R_S \Leftarrow \text{p-channel JFET} \end{aligned}\]
    \[\begin{aligned} \text{drain voltage}~V_D & = V_{DD} - I_D R_D \\ \text{drain-to-source voltage}~ V_{DS} & = V_{DD} - I_D (R_D + R_S) \\ \text{required source resistance}~R_S & = \left| \frac{V_{GS}}{I_D} \right| \end{aligned}\]

  • Biasing at the midpoint allows maximum current swing.

  • \[V_{GS} = V_{GS(\text{off})}/3.4\]
    , the gate-source voltage is: When

  • The Q-point is determined by plotting the load line.

  • \[V_{GS} = -I_D R_S\]
    The load line equation:

  • Intersection of load line and transfer characteristic gives \(I_D\) and \(V_{GS}\).

image

Voltage-Divider Bias

\[\begin{aligned} V_\mathrm{S} & =I_\mathrm{D}R_\mathrm{S} \\ V_\mathrm{G} & =\left(\frac{R_2}{R_1+R_2}\right)V_\mathrm{DD} \\ V_{\mathrm{GS}} & =V_{\mathrm{G}}-V_{\mathrm{S}} \Rightarrow~ V_\mathrm{S} =V_\mathrm{G}-V_\mathrm{GS} \\ I_{\mathrm{D}} & =\frac{V_{\mathrm{S}}}{R_{\mathrm{S}}} =\frac{V_{\mathrm{G}}-V_{\mathrm{GS}}}{R_{\mathrm{S}}} \end{aligned}\]

Current-Source Bias

  • Purpose: Increase Q-point stability by making \(I_\mathrm{D}\) independent of \(V_\mathrm{GS}\).

  • Method: constant-current source in series with the JFET source.

  • \[I_\mathrm{E} = \frac{V_\mathrm{EE} - V_\mathrm{BE}}{R_\mathrm{E}} \approx \frac{V_\mathrm{EE}}{R_\mathrm{E}}\]
    \(V_\mathrm{EE} \gg V_\mathrm{BE}\)\(I_\mathrm{E}\)Implementation

  • Result: \(I_\mathrm{D}\) remains constant across all transfer characteristic curves.

image

Ohmic Region in JFET Characteristics

  • Ohmic Region: Ohm’s law applies.

  • Behavior: JFET acts as a variable resistor.

  • Control: Resistance depends on \(V_{GS}\).

  • Extent: From origin to active region breakpoint.

  • Curves: Nearly constant slope for small \(I_D\).

    image

Slope and Conductance

  • The slope of the characteristic curve is related to the dc drain-to-source conductance \(G_{DS}\):

    \[\text{Slope} = G_{DS} \cong \dfrac{I_D}{V_{DS}}\]

  • The dc drain-to-source resistance is:

    \[R_{DS} = \dfrac{1}{G_{DS}} \cong \dfrac{V_{DS}}{I_D}\]

Biasing in the Ohmic Region

  • A JFET can be biased in either the active or ohmic region.

  • When biased in the ohmic region, the JFET is equivalent to a resistance.

  • When biased in the active region, the JFET is equivalent to a current source.

  • To bias in the ohmic region, the dc load line must intersect the characteristic curve.

  • For example, setting the dc saturation current:

    image
    • \[I_{D(sat)} = \dfrac{V_{DD}}{R_D} = \dfrac{12~\text{V}}{24~\text{k}\Omega} = 0.50~\text{mA}\]
  • \[\text{Decrease in slope} \implies \text{Less } I_D, \text{ More } V_{DS} \implies \text{Increase in } R_{DS}\]
    As Q-point moves along the load line, slope decreases, leading to:

  • This allows voltage-controlled resistance.