Produces DC output equal to peak value of rectified voltage
Most widely used in power supplies
Circuit Components: AC source, Diode, and Capacitor
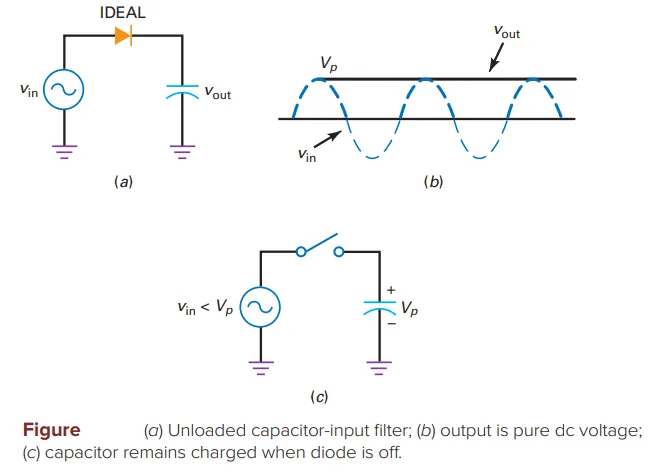
Operation:
Initially, capacitor is uncharged
During first quarter-cycle:
Diode forward biased, capacitor charges
Voltage across capacitor = Source voltage
Capacitor voltage = \(V_p\) (peak voltage)
After peak, diode turns off:
Capacitor stays charged
Output voltage = \(V_p\) (constant)
With Load Resistor:
Connect across capacitor
Capacitor remains charged if \(RLC\) time constant \(\gg\) period
Output voltage \(\approx V_p\) with small ripple
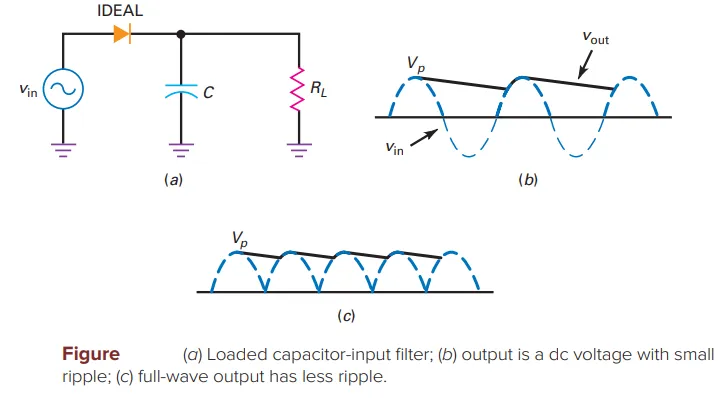
Ripple:
Diode off between peaks, capacitor discharges through load resistor
Capacitor supplies load current
Peak-to-peak ripple is small
Diode recharges capacitor to peak voltage when next peak arrives
Full-Wave or Bridge Rectifier:
Reduces peak-to-peak ripple by half
Capacitor discharges for half the time compared to half-wave rectifier
Ripple Formula: \[V_R = \frac{I}{f C}\]
\(V_R\) = Peak-to-peak ripple voltage
\(I\) = DC load current
\(f\) = Ripple frequency
\(C\) = Capacitance
Usage:
Approximation, not exact
Accurate results require circuit simulation (e.g., Multisim)
Given:
DC load current = 10 mA
Capacitance = 200 \(\mu\)F
Ripple frequency (bridge rectifier) = 120 Hz
Ripple Calculation: \[V_R = \frac{10 \text{ mA}}{120 \text{ Hz} \times 200 \mathrm{ \mu F}} = 0.417 \text{ V}_{\text{p-p}}\]
Measurement Methods:
Use oscilloscope for accurate measurement
AC voltmeter may introduce error (up to 25%)
Conversion: \[V_{\text{rms}} = \frac{V_{\text{p-p}}}{2 \sqrt{2}}\]
Converts peak-to-peak value to rms value
Factors Affecting DC Load Voltage:
Diode drops (subtract from peak voltage)
Additional voltage drop due to:
Heavy diode conduction during brief periods
Transformer winding and diode bulk resistance
Calculation:
Ideal output or output with diode approximation
Actual DC voltage is slightly lower
Problem: Half-wave rectifier and capacitor-input filter
What is the dc load voltage and ripple?
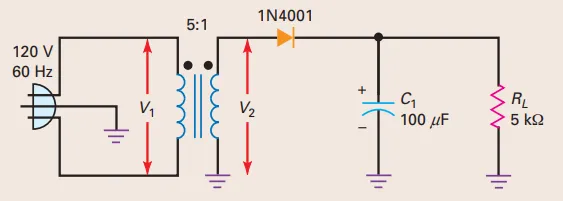
\[\begin{aligned} V_2 & =\frac{120 \mathrm{V}}{5}=24 \mathrm{V} \\ V_p & =\frac{24 \mathrm{V}}{0.707}=34 \mathrm{V} \\ V_{L} & =34 \mathrm{V}\\ I_L & =\frac{V_L}{R_L}=\frac{34 \mathrm{V}}{5 \mathrm{k}\Omega}=6.8 \mathrm{mA}\\ V_R & =\frac{6.8\text{ mA}}{(60\text{ Hz})(100 \mu\text{F})}=1.13\text{ V}_{\text{p-p}}\approx1.1\text{ V}_{\text{p-p}} \end{aligned}\]
Problem: Full-wave rectifier and capacitor-input filter
What is the dc load voltage and ripple?
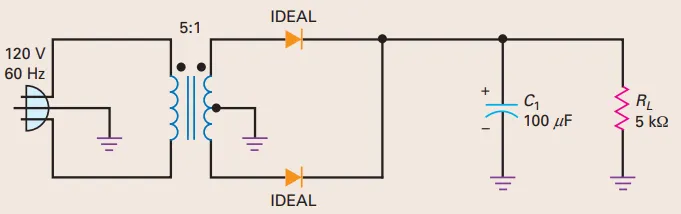
Transformer: \(5:1\) step-down
Peak secondary voltage: 34 V (previous problem)
Input to each halfwave section: 34 V / 2 = 17 V
DC load voltage (ideal diode, small ripple): 17 V
\[\begin{aligned} V_L & =17 \mathrm{~V} \\ I_L & =\frac{17 \mathrm{~V}}{5 \mathrm{k} \Omega}=3.4 \mathrm{~mA}\\ V_R & =\frac{3.4 \mathrm{~mA}}{(120 \mathrm{~Hz})(100 \mu \mathrm{F})}=0.283 \mathrm{~V}_{\mathrm{p}-\mathrm{p}} \approx 0.28 \mathrm{~V}_{\mathrm{p}-\mathrm{p}} \end{aligned}\]
Problem: Bridge rectifier and capacitor-input filter
What is the dc load voltage and ripple?
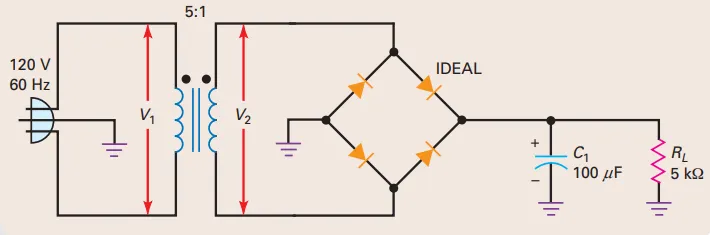
\[\begin{aligned} V_L & =34 \mathrm{~V} \\ I_L & =\frac{34 \mathrm{~V}}{5 \mathrm{k} \Omega}=6.8 \mathrm{~mA}\\ V_R & =\frac{6.8 \mathrm{~mA}}{(120 \mathrm{~Hz})(100 \mu \mathrm{F})}=0.566 \mathrm{~V}_{\mathrm{p}-\mathrm{p}} \approx 0.57 \mathrm{~V}_{\mathrm{p}-\mathrm{p}} \end{aligned}\]
Comparison & Conclusion:
\[\begin{aligned} \text{Half-wave:}~ & 34~\mathrm{V} ~ \text{and}~ 1.13 ~\mathrm{V} \\ \text{Full-wave:} ~& 17~\mathrm{V} ~ \text{and}~ 0.288 ~\mathrm{V} \\ \text{Bridge:}~ & 34~\mathrm{V} ~ \text{and}~ 0.566 ~\mathrm{V} \\ \end{aligned}\]
Bridge rectifier vs. half-wave rectifier: less ripple
Bridge rectifier vs. full-wave rectifier: twice the output voltage
Bridge rectifier: most popular