Bipolar Junction Transistor (BJT)- Biasing

Importance of BJT Biasing for Amplification

  • Definition:

    • BJT biasing involves setting up a transistor amplifier for desired operating conditions.

  • Purpose:

    • Establish the DC operating point.

    • Ensure stability against variations like temperature changes.

  • Amplifier Analysis Components:

    • DC Analysis: Determines steady-state operating point.

    • AC Analysis: Determines response to input signals.

  • Superposition Principle: DC and AC analyses can be handled separately.

  • Energy Transfer:

    • AC signal amplification is powered by energy from DC supplies.

  • Interdependence:

    • DC operating point affects AC response and vice versa.

Biasing and its Significance

  • Biasing: Application of DC voltages to establish a fixed current and voltage level.

  • Q-Point (Quiescent Point): The operating point on device characteristics where the system is stable and inactive without a signal.

  • Purpose: Enables the transistor to amplify input signals effectively.

  • Real-World Use Cases:

    • Audio amplifiers

    • RF circuits

    • Signal processing applications

Common Biasing Techniques

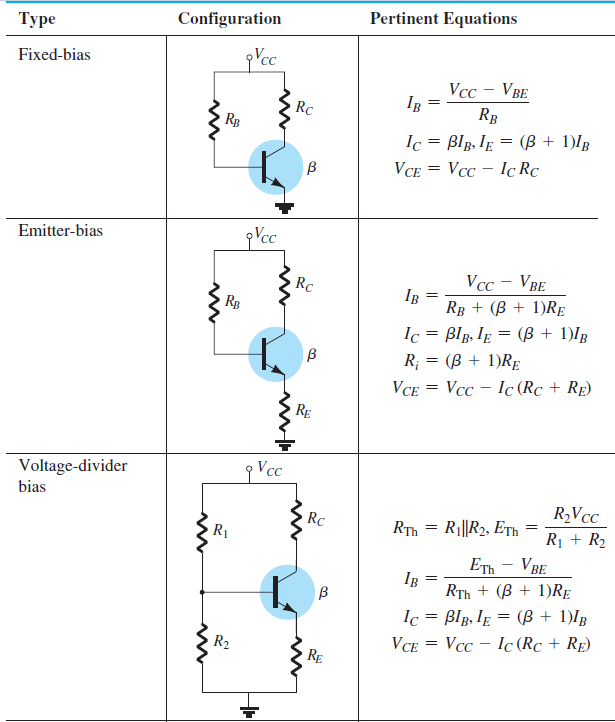
  • Fixed-Bias

  • Emitter-Bias

  • Voltage-Divider Bias

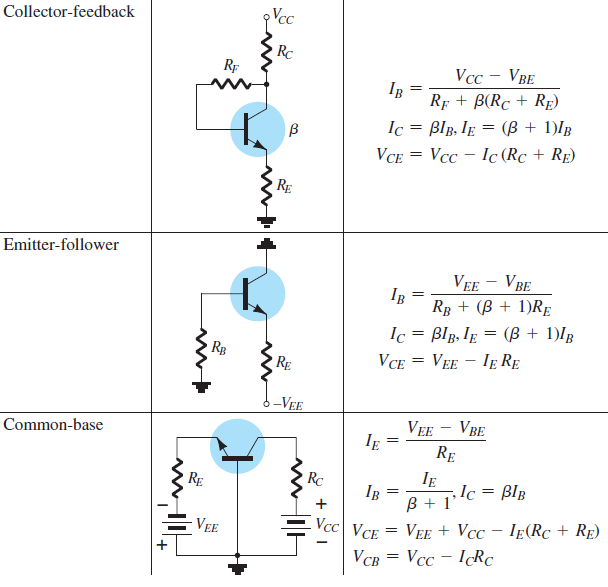
  • Collector Feedback

  • Emitter Follower

  • Common-Base

Revision of Important Facts

  • Basic Equations:

    • \(V_{BE} \approx 0.7 \, \text{V}\)

    • \(I_E = (\beta + 1) I_B \approx I_C\)

    • \(I_C = \beta I_B\)

  • Base current \(I_B\) is usually determined first.

  • Key Biasing Requirements for Amplification:

    1. Forward bias for base-emitter junction.

    2. Reverse bias for base-collector junction.

    3. Maintain operation in the active region for effective signal processing.

  • Impact of Temperature:

    • Increases leakage current \(I_{CEO}\).

    • Alters current gain \(\beta_{ac}\).

  • Stability Factor \(S\):

    • Measures the effect of temperature on the Q-point stability.

    • Higher stability is desirable.

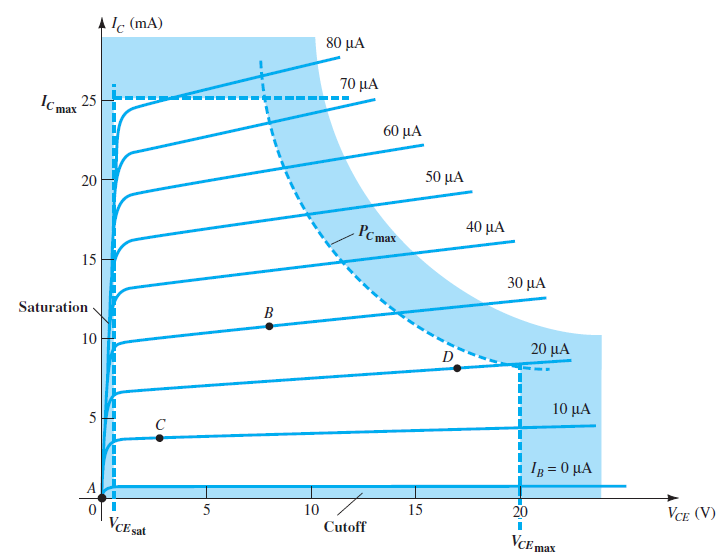
Q-Point Analysis

  • Operating Points:

    • Point A: Device completely OFF (unsuitable for amplification).

    • Point B: Ideal for small-signal amplification due to linear response.

    • Point C: Limited swing and nonlinear response.

    • Point D: High voltage operation, limiting positive voltage swing.

      image

    • Importance of Point B for Amplification

      • Ensures uniform amplification over signal swing.

      • Maintains consistent device gain.

      • Maximized at Point B without crossing into cutoff or saturation.

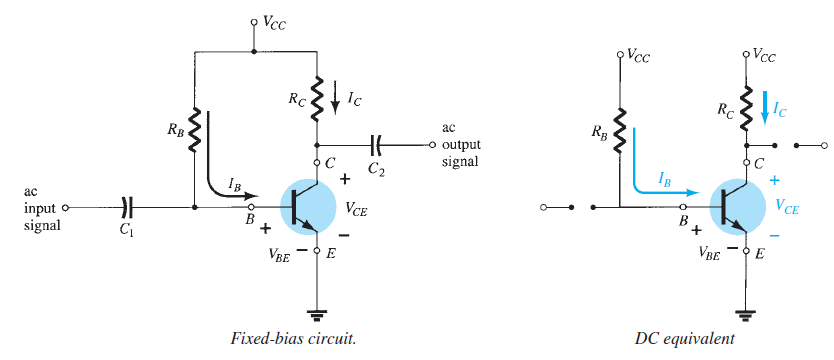
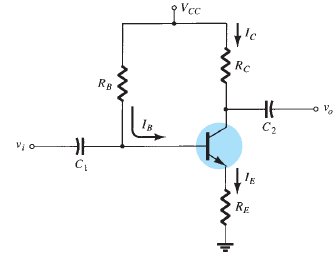
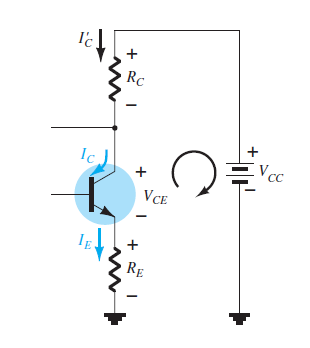
Fixed-Bias Configuration

  • Simplest DC bias configuration for a transistor.

  • Can be applied to both NPN and PNP transistors by changing current directions and voltage polarities.
    image

  • For DC Analysis AC sources are removed by replacing capacitors with open circuits.

  • \[X_C = \frac{1}{2\pi f C}\]
    \(X_C = \infty \, \Omega\)\(f = 0\) is split into input and output sections to simplify analysis. Supply

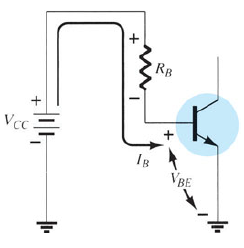
Base-Emitter Loop Analysis

  • \[+V_{CC} - I_B R_B - V_{BE} = 0\]
    Kirchhoff’s Voltage Law (KVL):
  • \[I_B = \frac{V_{CC} - V_{BE}}{R_B}\]
    Base Current Equation:

  • Key Insight: \(I_B\) is determined by \(R_B\) selection.

image

Collector-Emitter Loop Analysis

  • \[I_C = \beta I_B\]
    Current Relationship:
  • \[V_{CE} + I_C R_C - V_{CC} = 0 \quad \Rightarrow \quad V_{CE} = V_{CC} - I_C R_C\]
    KVL Application:

  • Observations: \(I_C\) is independent of \(R_C\) as long as the device remains in the active region. \(R_C\) affects the voltage \(V_{CE}\).

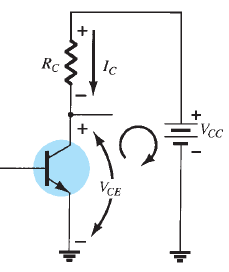
image

Important Relationships

  • \[V_{CE} = V_C - V_E = V_C\]
    Voltage Definitions:

  • Implications: \(V_E\) is often assumed as zero for simplicity. Control over \(V_{CE}\) is critical for setting the operating region.

image

Key Characteristics of Fixed-Bias Configuration

  • Simple to design and implement.

  • Provides control over base current through \(R_B\).

  • Sensitive to variations in \(\beta\) and temperature changes.

  • Primarily suited for low-power or stable environments.

Limitations and Stability Concerns

  • High sensitivity to temperature variations and transistor parameters.

  • Lack of automatic stabilization makes it less suitable for high-precision applications.

  • Improved configurations like voltage-divider bias address these concerns.

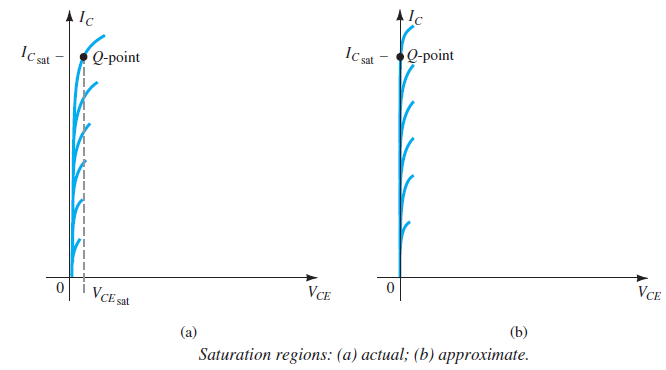
What is Saturation in Transistors?

  • Definition:

    • A system is in saturation when it operates at maximum levels.

    • Similar to a sponge fully soaked with water, unable to hold more.

  • In Transistors:

    • Current reaches a maximum for the design.

    • \(V_{CE}\) approaches or equals \(V_{CE_{\text{sat}}}\).

    • Base–collector junction no longer reverse-biased, leading to distortion.

Saturation Characteristics

  • \(V_{CE} \approx 0~\mathrm{V}\)

  • Collector current at maximum \(I_{C_{\text{sat}}}\).

  • High \(I_C\) and low voltage across collector-emitter terminals.

  • Point where characteristic curves converge (Fig.).
    image

  • Treat the collector-emitter path as a short circuit.

  • Calculate the resulting \(I_C\) by assuming \(V_{CE} = 0~\mathrm{V}\).

    \[R_{CE} = \frac{V_{CE}}{I_C} = \frac{0~\mathrm{V}}{I_{C_{\text{sat}}}} = 0~\Omega\]

Determining Saturation Current

  • Apply a short circuit between collector and emitter.

  • Voltage across \(R_C\) becomes \(V_{CC}\).

    \[I_{C_{\text{sat}}} = \frac{V_{CC}}{R_C}\]

  • \(I_C\) should remain below \(I_{C_{\text{sat}}}\) for linear amplification.

Importance of Avoiding Saturation

  • Distortion Risk:

    • Saturation disrupts linear amplification, introducing signal distortion.

  • Design Considerations:

    • Ensure \(I_C\) operates well below \(I_{C_{\text{sat}}}\) for clean amplification.

  • Practical Applications:

    • Avoiding saturation ensures consistent and accurate signal amplification.

Emitter-Bias Configuration

  • Objective: Improve stability over fixed-bias configuration.

  • Key Features:

    • Addition of emitter resistor \(R_E\).

    • Greater resistance to temperature variations and parameter shifts.

  • Application: Used for circuits requiring consistent performance under varying conditions.

    image

  • \(R_E\) introduces feedback that stabilizes the circuit.

  • \(R_E\) impacts both base and collector-emitter loops.

Base–Emitter Loop Analysis

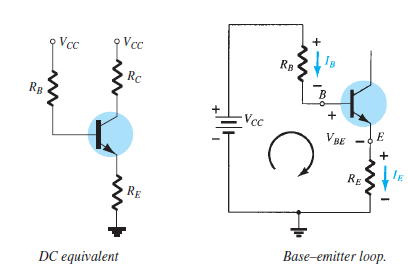
image
\[\begin{aligned} & +V_{CC} - I_B R_B - V_{BE} - I_E R_E = 0\\ & I_E = (\beta + 1) I_B \\ & I_B = \frac{V_{CC} - V_{BE}}{R_B + (\beta + 1) R_E} \end{aligned}\]

  • Compared to Fixed-Bias the additional term \((\beta + 1) R_E\) in the denominator improves stability.

Equivalent Circuit and Reflection Concept

  • \(R_E\) appears in base circuit as \((\beta + 1) R_E\) due to reflection effect.

  • Significantly larger apparent resistance due to \(\beta\) (50 or more).

    \[\text{Input Resistance}~R_i = (\beta + 1) R_E\]

  • Greater \(R_i\) offers better temperature stability and reduces sensitivity to variations in \(\beta\).

    image

Collector–Emitter Loop Analysis

\[\begin{aligned} & + I_E R_E + V_{CE} + I_C R_C - V_{CC} = 0 \\ & I_E \approx I_C \\ & V_{CE} = V_{CC} - I_C(R_C + R_E) \end{aligned}\]
image
\[\begin{aligned} & V_E = I_E R_E \\ & V_C = V_{CE} + V_E \quad \text{or} \quad V_C = V_{CC} - I_C R_C \\ & V_B = V_{CC} - I_B R_B \quad \text{or} \quad V_B = V_{BE} + V_E \end{aligned}\]

Voltage Levels and Biasing Points

  • Maintaining \(V_{CE}\) above saturation voltage ensures linear operation.

  • Proper selection of \(R_E\) and \(R_C\) determines \(V_{CE}\) and enhances stability.

  • Stabilizes operating point by providing negative feedback.

  • Ensures consistent operation despite changes in temperature or transistor parameters.

Voltage-Divider Bias

  • Biasing in BJTs sets the operating point (Q-point) for consistent performance.

  • Previous configurations depend on transistor’s current gain (\(\beta\)).

  • \(\beta\) is temperature-sensitive and varies, especially in silicon transistors.

  • Desire for bias circuits less dependent on \(\beta\).

  • Voltage-divider bias provides stable operating points despite \(\beta\) variations.

  • Proper circuit parameters lead to \(\beta\) independence for \(I_{CQ}\) and \(V_{CEQ}\).

Circuit Configuration

image

  • Resistors \(R_1\) and \(R_2\) form a voltage divider.

  • Bias point defined by \(I_{CQ}\) and \(V_{CEQ}\) stays stable.

  • Despite changes in \(\beta\), \(I_{CQ}\) and \(V_{CEQ}\) can remain fixed.

Analysis

\[\begin{aligned} R_{TH} & = R_1 || R_2 \qquad E_{TH} = V_{R_2} = \dfrac{R_2V_{CC}}{R_1+R_2} \\ &E_{TH} -I_BR_{TH}-V_{BE}-I_ER_E=0 \\ I_E &=(\beta+1)I_B,~\text{we get}\\ I_B & = \dfrac{E_{TH}-V_{BE}}{R_{TH}+(\beta+1)R_E} \\ V_{CE} & = V_{CC}-I_C(R_C+R_E) \\ \end{aligned}\]
image

  • \(V_E\), \(V_C\), and \(V_ B\) are same as obtained for the emitter-bias.

Benefits of Voltage-Divider Bias

  • Minimizes temperature and \(\beta\) sensitivity.

  • Stable Q-point ensures consistent circuit performance.

  • Versatile and widely used in practical designs.

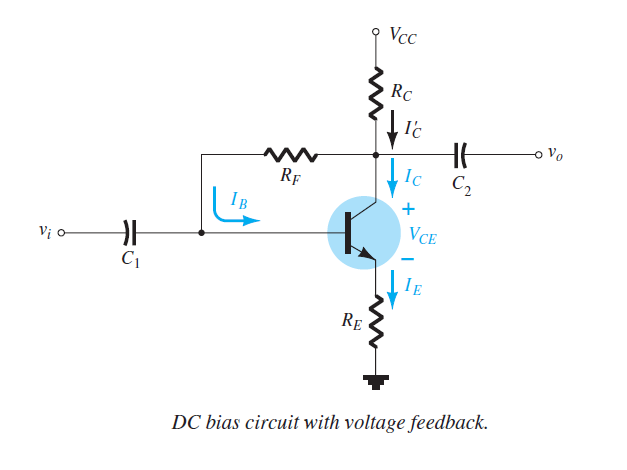
Collector Feedback Configuration

  • An improved level of stability by introducing a feedback path from collector to base

    image

  • The Q-point is less sensitive to \(\beta\) and temperature changes than other biasing methods.

  • Base–Emitter Loop:

    image
    \[\begin{aligned} \text{KVL}~& V_{CC} - I_{C}^{\prime}R_C - I_BR_F - V_{BE} - I_ER_E =0 \\ &I_{C}^{\prime} = I_{C} + I_{B} \\ \text{Normally} ~& I_{C}^{\prime} \cong I_{C} = \beta I_B \quad I_E \cong I_{C} \\ \therefore ~ & V_{CC} - \beta I_B R_C - I_BR_F - V_{BE} - \beta I_B R_E =0 \\ \Rightarrow ~& I_B = \dfrac{V_{CC} - V_{BE} }{R_F + \beta (R_C + R_E)} \end{aligned}\]
  • \[I_B = \dfrac{V^\prime}{R_F + \beta R^{\prime}}\]
    In general,

  • For fixed-bias configuration \(\Rightarrow~\beta R^\prime\) does not exist

  • For the emitter-bias \(\Rightarrow~\beta+1 \cong \beta \qquad R^\prime = R_E\)

  • \[\begin{aligned} I_{CQ} & = \dfrac{\beta V^{\prime}}{R_F + \beta R^{\prime}} = \dfrac{V^\prime}{\dfrac{R_F}{\beta}+R^{\prime}} \\ &\cong \dfrac{V^\prime}{R^\prime}~ \left(\because R^\prime >> \dfrac{R_F}{\beta} \right) \\ \Rightarrow ~& \text{Independent of } \beta ~\text{variation} \end{aligned}\]
    , Because

  • Collector–Emitter Loop:

    image
    \[\begin{aligned} \text{KVL}~& I_ER_E + V_{CE} + I_C^{\prime}R_C - V_{CC} =0 \\ \Rightarrow~& I_C (R_C + R_E) + V_{CE} - V_{CC} = 0 ~(\because ~I_C^\prime \cong I_C \quad I_E \cong I_C ) \\ \Rightarrow~& V_{CE} = V_{CC} - I_C (R_C + R_E)\\ \Rightarrow~& \text{Exactly same as emitter-bias and voltage-divider bias} \end{aligned}\]

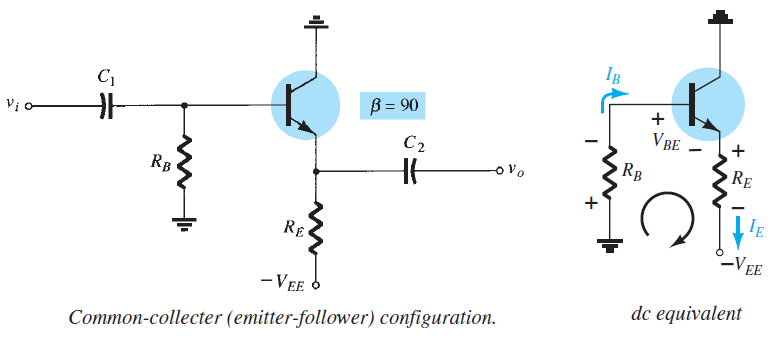
EMITTER-FOLLOWER CONFIGURATION

  • In collector-feedback, \(V_0\) is taken from collector terminal.

  • In emitter-follower, the output is taken off the emitter terminal.
    image
    \[\begin{aligned} \text{KVL}\quad & -I_BR_B - V_{BE} -I_ER_E + V_{EE} = 0\\ \text{Using} \quad & I_E = (\beta+1)I_B \\ \Rightarrow~& I_BR_B + (\beta+1)I_BR_E = V_{EE} - V_{BE} \\ \Rightarrow~& I_B = \dfrac{V_{EE} - V_{BE}}{R_B + (\beta+1)R_E} \end{aligned}\]
  • \[V_{CE} = V_{EE} - I_E R_E\]
    Output network:

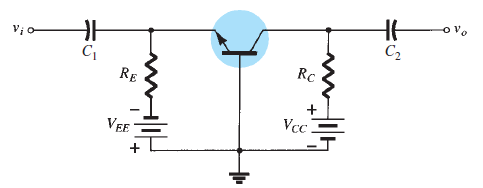
COMMON-BASE CONFIGURATION

  • Input signal is connected to the emitter terminal.

  • The base is held at ground or just above ground potential.

  • The common-base configuration is unique due to the use of two supplies and its design where the base is the common terminal.

  • Advantages: low input impedance, high output impedance, and good gain.

    image
  • \[\begin{aligned} & -V_{EE}+I_ER_E+V_{BE}=0 \\ & I_E=\frac{V_{EE}-V_{BE}}{R_E} \end{aligned}\]
    Input dc equivalent:

  • Determining \(V_{CE}\) and \(V_{CB}\):

    \[\begin{aligned} &-V_{EE}+I_{E}R_{E}+V_{CE}+I_{C}R_{C}-V_{CC}=0\\ &I_{E}\cong I_{C} \\ &\boxed{V_{CE}=V_{EE}+V_{CC}-I_E(R_C+R_E)} \\ V_{CB}&=V_{CC}-I_{C}R_{C}\\ I_{C}&\cong I_{E} \\ & \boxed{V_{CB}=V_{CC}-I_CR_C} \end{aligned}\]

Summary

image
image