Solved Problems on Single-Phase Induction Motors
Problem-1
A 6-pole, 50-Hz, 1-phase induction motor runs at a speed of 900 rpm. Determine the frequency of currents in the cage rotor?
Solution
\[\begin{aligned} N_s & =\frac{120f}{P}=\frac{120\times50}{6}=1000 ~\mathrm{rpm} \\ \text{Slip,}~s & =\frac{1000-900}{1000}=0.1=10\% \\ \end{aligned}\]
The two rotor current frequencies are :
\[\begin{aligned} sf & =0.1\times50=5 ~\mathrm{Hz}\\ (2-s)f & =1.9\times50=95 ~\mathrm{Hz} \end{aligned}\]
Problem-2
For a single-phase motor of 2 HP rating, supply voltage is 240 V ac. If the efficiency is 70% and power factor is 0.8, find the input current.
Solution
\[\begin{aligned} 1~\mathrm{HP} & = 746~\mathrm{W} \\ P_{\text{out}}& = 2~\mathrm{HP} = 2 \times 746 = 1492~\mathrm{W} \\ \text{Input Power}~ (P) & = \frac{\text{Output power}}{\eta}= \frac{1492}{0.7}\\ &=2131.43 ~\mathrm{W} \\ \Rightarrow~2131.43 & =240\times1\times0.8\\ \Rightarrow~ I & =11.1 ~\mathrm{A} \end{aligned}\]
Problem-3
A 4-pole single-phase induction motor is rotating in a clockwise direction at a speed of 1000 rpm having a voltage of 100 V with a frequency of 50 Hz. At a standstill, if the rotor resistance is 1.7 \(\Omega\), then in the backward branch what will be the effective resistance?
Solution
The effective rotor resistance in the forward branch \(\left(R_f\right)\)
\[R_f=\frac{R_2^{\prime}}{2 s}\]
The effective rotor resistance in the backward branch \(\left(R_b\right)\)
\[R_b=\frac{R_2^{\prime}}{2(2-s)}\]
Where \(R_2{ }^{\prime}=\) Standstill rotor resistance referred to as the main stator winding.
\[\begin{aligned} N_s & =\frac{120\times50}4 = 1500~\mathrm{rpm}\\ s & =\frac{1500-1000}{1500}=\frac{500}{1500} = 0.33 \\ R_{b} & =\frac{1.7}{2(2-0.33)}\\ &=\frac{1.7}{2\times1.67}\approx0.5~ ~\Omega \end{aligned}\]
Problem-4
A 6 pole, 50 Hz induction motor has an equivalent rotor resistance of 0.01 \(\Omega\)/phase. If its stalling speed is 900 rpm, determine the resistance that must be inserted in rotor windings per phase to obtain maximum torque at starting?
Solution
\[\begin{aligned} \text{Synchronous speed},~ Ns & =120 \times 50/6=1000 ~\mathrm{rpm} \\ \text{Stalling speed} & = 900 ~\mathrm{rpm} \\ \text{Slip at stalling speed}, s & =1000-900/1000=0.1 \\ \end{aligned}\]
\[\begin{aligned} &\text { Slip at maximum torque; }\\ &\begin{aligned} & \mathrm{SmT}=\mathrm{R}_2 / \mathrm{X}_2=0.01 / \mathrm{X}_2 \\ & \because 0.1=0.01 / \mathrm{X}_2 \\ \Rightarrow& \mathrm{X}_2=0.1~ ~\Omega \end{aligned} \end{aligned}\]
To obtain maximum torque at starting
Rotor resistance \(=\mathrm{R}^{\prime}_2\) at starting \(\mathrm{s}=1\)
\[\begin{aligned} \mathrm{S}_m&=\mathrm{R}^{\prime} 2 / \mathrm{X}_2 \\ \Rightarrow 1 & =R_2^{\prime} / 0.1\\ \Rightarrow R^{\prime}{ }_2 & =0.1 ~\Omega / \text{phase} \\ R_{ext} &=0.1-0.01\\ &=0.09 ~\Omega / \text{phase} \end{aligned}\]
Problem-5
A single phase, \(230 \mathrm{~V}, 50 \mathrm{~Hz}\), 4 pole, capacitor start induction motor has the following standstill impedance.
\[\begin{aligned} \text{Main winding}: \mathrm{Zm} & =(8.0+j 5.0)~ ~\Omega \\ \text{auxiliary winding}: \mathrm{Za} & =(9.0+\mathrm{j} 6.0) ~\Omega \end{aligned}\]
Determine the value of the starting capacitor required to produce \(90^{\circ}\) phase difference between the current in the main and auxiliary windings.
Solution
\[\begin{aligned} \text{Main winding}~Z_m&=(8.0+j5.0)\Omega =9.434\angle32^{\circ}~\Omega \\ \text{Auxiliary winding}~Z_a & =(9.0+j6.0)~\Omega=10.82\angle33.69^\circ~\Omega \end{aligned}\]
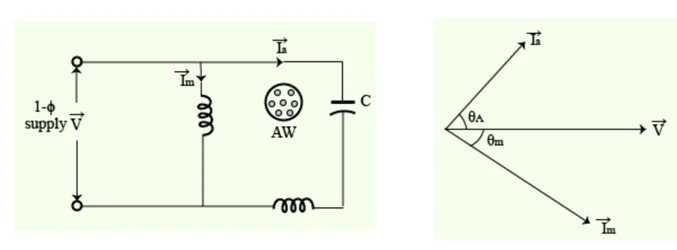
\(\overrightarrow{I_m}\) lags behind voltage \(\vec{V}\) by angle \(\theta_m = 32^{\circ}\)
Total impedance of auxiliary winding : \[\begin{aligned}&\overrightarrow{Z_{\mathrm{aw}}}=\overrightarrow{Z_{\mathrm{a}}}+\frac{1}{\mathrm{j\omega C}}\\&=9-\mathrm{j} (\frac{1}{\omega C}-6)=Z_{\mathrm{aw}}\angle-\theta_{a} \\ \theta_{a} & =\tan^{-1}\frac{(\frac{1}{\omega C}-6)}{9} \end{aligned}\]
Phase difference :
\[\begin{aligned} &\theta_{m} +\theta_{a} =90^{\circ}\\ &\tan^{-1}\left(\frac{\frac1{\omega C}-6}{9}\right)+32^{\circ}=90^{\circ} \Rightarrow& \frac{1}{\omega C}=20.4 \end{aligned}\]
\[C=\frac{1}{2\pi\times50\times20.4}=156.03~ \mu F\]
Problem-6
A 120 V, 60 Hz, single-phase induction motor of the capacitor-start type has a main winding with 180 effective turns and an auxiliary starting winding with 250 effective turns. With the rotor stationary, the input impedance of the main winding is \(5+j10~\Omega\) and that of the auxiliary winding is \(13.89 + j15.50~\Omega\).
Determine at standstill:
The magnitude of the forward and backward-rotating fields
The size of the starting capacitor necessary to yield a single rotating magnetic field at starting.
Solution
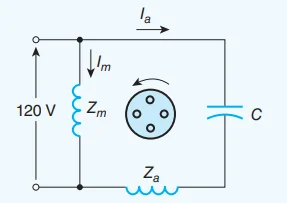
The positive (\({F}_{m_1}\)) and negative (\({F}_{m_2}\)) sequence components of the motor’s mmf:
\[\begin{bmatrix}{F}_{m_1}\\{F}_{m_2}\end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1 & -j \\ 1 & j \end{bmatrix} \begin{bmatrix} N_m I_m \\ N_a I_a \end{bmatrix}\]
\[\begin{aligned} {F}_{m_1} & =\frac{1}{2}\left(N_m I_m-j N_a I_a\right) \\ & =\frac{1}{2}(120)\left(\frac{180}{5+j 10}-j \frac{250}{13.89+j 15.50}\right) \\ & =1349.10 \angle-94.5^{\circ} \mathrm{A} \mathrm{rms} \\ {F}_{m_2} & =\frac{1}{2}\left(N_m I_m+j N_a I_a\right) \\ & =\frac{1}{2}(120)\left(\frac{180}{5+j 10}+j \frac{250}{13.89+j 15.50}\right) \\ & =1041.7 \angle-21.6^{\circ} \mathrm{A} \mathrm{rms} \end{aligned}\]
The positive-sequence component of the auxiliary winding’s mmf \[{F}_{a_1}=j{F}_{m_1}=1349.10\angle{-4.5^\circ}\text{A rms}\]
the negative-sequence component \[{F}_{a_2}=-j{F}_{m_2}=1041.7\angle{-111.6^\circ}\text{A rms}\]
Thus, the net forward-rotating field is
\[\begin{aligned} {F}_1={F}_{a_1}+j {F}_{m_1} & =1349.1\left(1 \angle-4.5^{\circ}+1 \angle-4.5^{\circ}\right) \\ & =2,698.2 \angle-4.5^{\circ} \mathrm{A} \mathrm{rms} \end{aligned}\]
The net backward-rotating field is
\[\begin{aligned} {F}_2={F}_{a_2}+j {F}_{m_2} & =1041.7\left(1 \angle-111.6^{\circ}+1 \angle-21.6^{\circ}\right) \\ & =90.9~ \angle 155.9^{\circ} \mathrm{A} \mathrm{rms} \end{aligned}\]
To have a single rotating field, the backward-rotating mmf must be equal to zero. That is,
\[\frac{1}{2}(120)\left(\frac{180}{5+j 10}+j \frac{250}{Z_a}\right)=0\]
The impedance of the auxiliary winding is
\[Z_a=13.89+j\left(15.5-X_c\right)\]
where \(X_c\) is the reactance of the capacitor.
From the last two relationships,
\[\begin{aligned} Z_a & =-j\left(\frac{250(5+j 10)}{180}\right)=13.89+j\left(15.5-X_c\right) \\ X_c &=22.44 ~\Omega\\ \Rightarrow~C & =\frac{1}{\omega X_c} =\frac{1}{2 \pi(60)(22.44)} =118.2 \mu \mathrm{F} \end{aligned}\]