Demonstrative Video
Problem-1
The magnetic structure of a synchronous machine has the stator and rotor iron of infinite permeability (\(\mu_r=\infty\)). Find
air-gap flux (\(\phi\))
flux density (\(B_g\)).
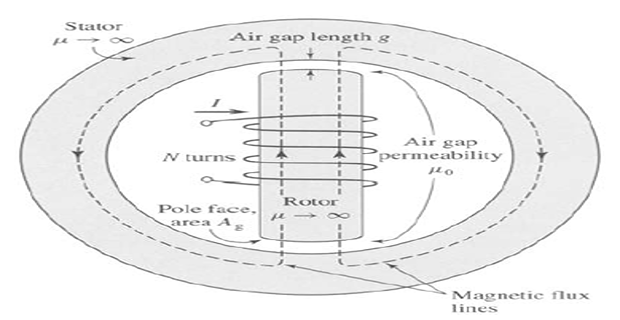
Consider \(I=10~A\), \(N=1000\) turns, \(g=1\) cm, and \(A_g=2000~\text{cm}^2\).
Solution-1
Notice that there are two air gaps in series, of total length \(2 g,\) and that by symmetry the flux density in each is equal.
Since the iron \(\mu_r=\infty\), its reluctance is negligible and \(g\) replaced by the total gap length \(2 g\) can be used to find the flux
\[\begin{aligned} \phi&=\frac{N I \mu_{0} A_{g}}{2 g}=\frac{1000(10)\left(4 \pi \times 10^{-7}\right)(0.2)}{0.02}=0.13 \mathrm{~Wb} \\ B_{g}&=\frac{\phi}{A_{g}}=\frac{0.13}{0.2}=0.65 \mathrm{~T} \end{aligned}\]
Problem-2
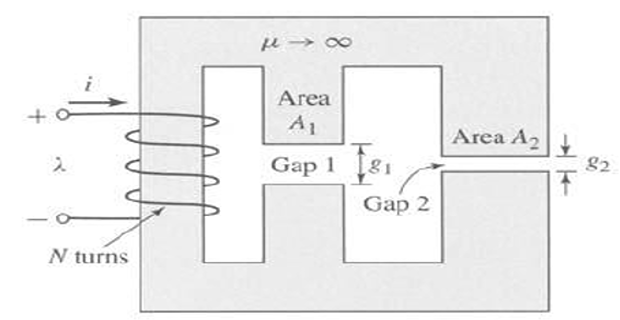
The magnetic circuit consists of an N-turn winding on a magnetic core of infinite permeability with two parallel air gaps of length \(g_1\) and \(g_2\), and areas \(A_1\) and \(A_2\), respectively. Find
the inductance of the winding and
the flux density \(B_1\) in gap-1 when the winding is carrying a current \(i\)
Neglect fringing effects at the air-gap.
Solution-2
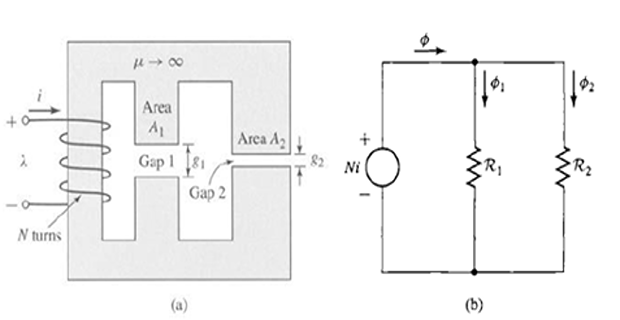
Total reluctances is equal to the parallel combination of the two gap reluctances. \[\phi=\frac{N i}{\frac{R_{1} R_{2}}{R_{1}+R_{2}}} \quad \mathcal{R}_1 = \dfrac{g_1}{\mu_0A_1} \quad \mathcal{R}_2=\dfrac{g_2}{\mu_0A_2}\]
\[\begin{aligned} L &=\frac{\lambda}{i}=\frac{N \phi}{i}=\frac{N^{2}\left(\mathcal{R}_{1}+\mathcal{R}_{2}\right)}{\mathcal{R}_{1} \mathcal{R}_{2}} =\mu_{0} N^{2}\left(\frac{A_{1}}{g_{1}}+\frac{A_{2}}{g_{2}}\right) \end{aligned}\]
From equivalent circuit \[\begin{array}{c} \phi_{1}=\dfrac{N i}{\mathcal{R}_{1}}=\dfrac{\mu_{0} A_{1} N i}{g_{1}} \\ B_{1}=\dfrac{\phi_{1}}{A_{1}}=\dfrac{\mu_{0} N i}{g_{1}} \end{array}\]
Problem-3
Find
Inductance, \(L\)
Magnetic stored energy \(W\) for \(B_c=1.0~T\)
Induced volatge \(e\) for a 60-Hz time varying core flux of the form \(B_c=1.0\sin\omega t\) T where \(2\pi 60=377\)
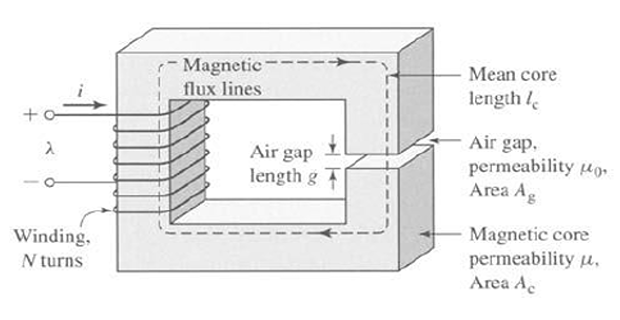
Solution-3
\[\begin{aligned} L &=\frac{\lambda}{i}=\frac{N \phi}{i}=\frac{N^{2}}{\mathcal{R}_{\mathrm{c}}+\mathcal{R}_{g}} \\ &=\frac{500^{2}}{4.46 \times 10^{5}}=0.56 \mathrm{H} \end{aligned}\] Note that the core reluctance is much smaller than that of the gap \(\left(\mathcal{R}_{\mathrm{c}} \ll \mathcal{R}_{g}\right)\). Thus to a good approximation the inductance is dominated by the gap reluctance, i.e., \[L \approx \frac{N^{2}}{\mathcal{R}_{g}}=0.57 \mathrm{H}\]
we found that when \(B_{\mathrm{c}}=1.0 \mathrm{~T}, i=0.80 \mathrm{~A}\). Thus \[W=\frac{1}{2} L i^{2}=\frac{1}{2}(0.56)(0.80)^{2}=0.18 \mathrm{~J}\]
\[\begin{aligned} e &=\frac{d \lambda}{d t}=N \frac{d \varphi}{d t}=N A_{c} \frac{d B_{\mathrm{c}}}{d t} \\ &=500 \times\left(9 \times 10^{-4}\right) \times(377 \times 1.0 \cos (377 t)) \\ &=170 \cos (377 t) \quad V \end{aligned}\]
Problem-4
\[\begin{aligned} A_{c}&=A_{g}=9~\mathrm{cm}^{2}\\ g&=0.050 \mathrm{~cm}\\ l_{c}&=30 \mathrm{~cm} \\ N&=500~ \text{turns} \end{aligned}\]
The core material has the dc magnetization curve as shown in the Fig.
Find the current \(I\) required to
produce \(B_c = 1 ~T\).
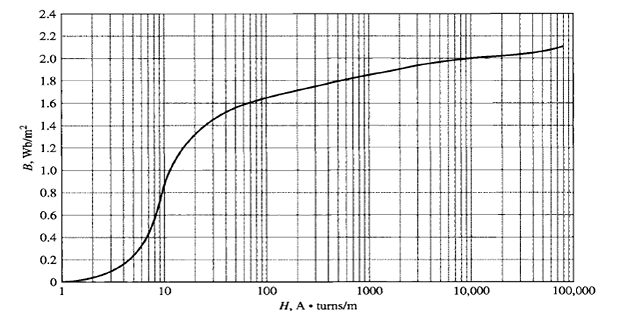
Solution-4
The value of \(H_{\mathrm{c}}\) for \(B_{\mathrm{c}}=1 \mathrm{~T}\) is read from Fig. as \[H_{\mathrm{c}}=11 \mathrm{~A} \cdot \text { turns } / \mathrm{m}\]
The \(\mathrm{mmf}\) drop for the core path is \[\mathcal{F}_{\mathrm{c}}=H_{\mathrm{c}} l_{\mathrm{c}}=11(0.3)=3.3 \mathrm{~A} \cdot \text { turns }\]
The mmf drop across the air gap is \[\mathcal{F}_{g}=H_{g} g=\frac{B_{g} g}{\mu_{0}}=\frac{5 \times 10^{-4}}{4 \pi \times 10^{-7}}=396 \mathrm{~A} \cdot \text { turns }\]
The required current is \[i=\frac{\mathcal{F}_{\mathrm{c}}+\mathcal{F}_{\mathrm{g}}}{N}=\frac{399}{500}=0.80 \mathrm{~A}\]
Problem-5
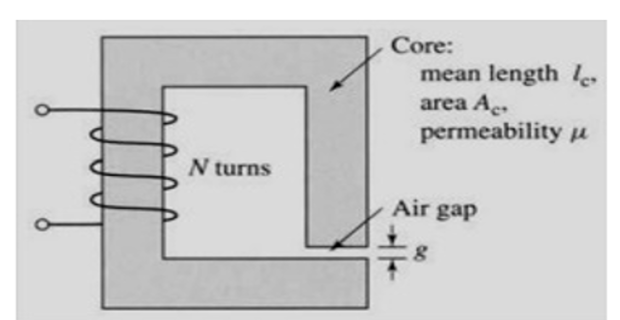
Given: Core \(A_{c}=1.8 \times 10^{-3} \mathrm{~m}^{2},\) \(I_{c}=0.6 \mathrm{~m},\) \(g=2.3 \times 10^{-3} \mathrm{~m}, ~N=83\) turns. Assume core is of \(\mu=\infty\) and neglect the effects of fringing fields at the air gap and leakage flux.
Calculate \(\mathcal{R}_{\mathrm{c}}\) and \(\mathcal{R}_{\mathrm{g}}\)
For a current of \(\mathrm{i}=1.5 \mathrm{~A},\) calculatetotal flux \(\phi\), flux linkages \(\lambda\) of the coil, and coil inductance L.
\(N\) required to achieve an inductance of \(12 \mathrm{mH}\)
the inductor current which will result in \(B_c\) of \(1.0 \mathrm{~T}\).
Solution-5
\(R_{c}=0 \text { since } \mu \rightarrow \infty\) \[\begin{array}{l} R_{g}=\dfrac{g}{\mu_{0} A_{c}}=\dfrac{2.3 \times 10^{-3}}{4 \pi \times 10^{-7} \times 1.8 \times 10^{-3}}=1.017 \times 10^{6} \mathrm{~A} / \mathrm{Wb} \end{array}\] \[\begin{aligned} \phi=& \dfrac{N i}{R_{c}+R_{g}}=\dfrac{83 \times 1.5}{1.017 \times 10^{6}}=1.224 \times 10^{-4} \mathrm{~Wb} \\ \lambda &=N \phi=1.016 \times 10^{-2} \mathrm{~Wb} \\ L=\dfrac{\lambda}{i} &=\dfrac{1.016 \times 10^{-2}}{1.5}=6.773 \mathrm{mH} \end{aligned}\]
\[\begin{aligned} L&=\dfrac{N^{2}}{R_{g}}=12 \times 10^{-3} \mathrm{mH} \\ &\Rightarrow N=\sqrt{12 \times 10^{-3} \times 1.017 \times 10^{6}}=110.47 \Rightarrow N=110 \text { turns } \\ B_{c}&=B_{g}=1.0 \mathrm{~T} \Rightarrow \phi=B_{g} A_{c}=1.8 \times 10^{-3} \mathrm{~Wb} \\ i&=\dfrac{\lambda}{L}=\dfrac{N \phi}{L}=\frac{110 \times 1.8 \times 10^{-3}}{12 \times 10^{-3}}=16.5 \mathrm{~A} \end{aligned}\]
Problem-6
find the flux density and flux in each of the outer limbs and the central limbs. Assume \(\mu_r\) for iron of the core to be (a) \(\infty\) (b) 4500.
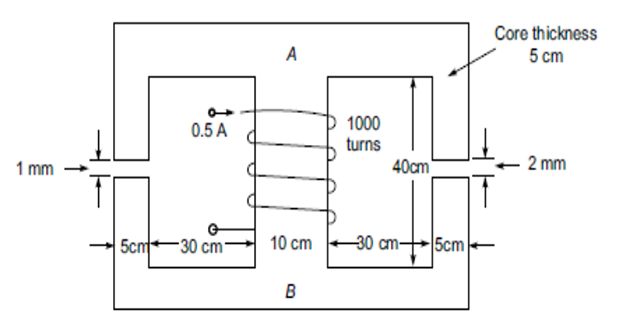
Solution-6
\[\begin{aligned}
\mu_{\mathrm{r}}&=\infty \\
N_{1}&=1000 \times 0.5=500 \mathrm{AT}\\
R_{\mathrm{g} 1}&=\frac{2 \times 10^{-3}}{4 \pi \times 10^{-7}
\times 25 \times 10^{-4}}\\
&=0.6366 \times 10^{6} \mathrm{AT} / \mathrm{Wb} \\
R_{\mathrm{g} 2}&=\frac{1 \times 10^{-3}}{4 \pi \times 10^{-7}
\times 25 \times 10^{-4}}\\
&=0.3183 \times 10^{6} \mathrm{AT} / \mathrm{Wb}
\end{aligned}\]
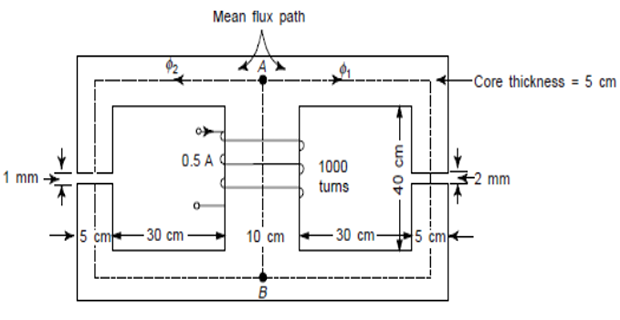 \[\phi_{1}=\frac{500}{0.6366 \times 10^{6}}=0.785
\mathrm{mWb}\]
\[\phi_{1}=\frac{500}{0.6366 \times 10^{6}}=0.785
\mathrm{mWb}\]
\[\begin{aligned} B_{1}&=\dfrac{0.785 \times 10^{-3}}{25 \times 10^{-4}}=0.314 \mathrm{~T} \\ \phi_{2}&=\dfrac{500}{0.3183 \times 10^{6}}=1571 \mathrm{mWb} \\ B_{2}&=\dfrac{157 \times 10^{-3}}{25 \times 10^{-4}}=0.628 \mathrm{~T} \\ \phi&=\phi_{1}+\phi_{2}=2.356 \mathrm{mWb} \\ B&=\dfrac{2.356 \times 10^{-3}}{50 \times 10^{-4}}=0.471 \mathrm{~T} \end{aligned}\]
\(\mu_{\mathrm{r}}=4,500 .\) The corresponding analogous electrical circuit is given in Fig. Effect of air-gaps on iron path length is negligible.
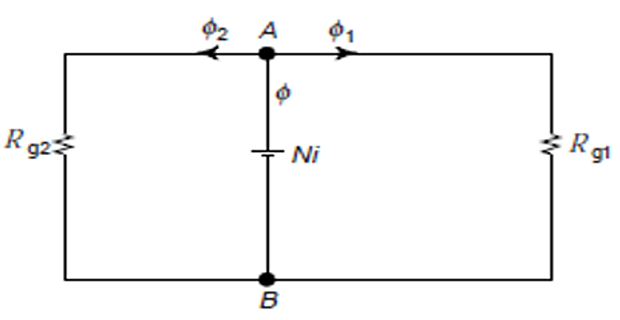
\[\begin{aligned} l_{\mathrm{cl}}&=l_{\mathrm{C} 2}=(40+5)+2 \times(30+5+2.5)=120 \mathrm{~cm} \\ R_{\mathrm{cl}}&=R_{\mathrm{C} 2}=\frac{120 \times 10^{-2}}{4 \pi \times 10^{-7} \times 4,500 \times 25 \times 10^{-4}}=0.085 \times 10^{6} \mathrm{AT} / \mathrm{Wb} \\ l_{\mathrm{c} 3}&=40+5=45 \mathrm{~cm} \\ R_{\mathrm{c} 3} &=\frac{45 \times 10-2}{4 \pi \times 10^{-7} \times 4,500 \times 50 \times 10^{-4}}=0.016 \times 10^{6} \mathrm{AT} / \mathrm{Wb} \\ R_{\mathrm{eq}} &=\left[\left(R_{\mathrm{cl}}+R_{\mathrm{g} 1}\right) \|\left(R_{\mathrm{c} 2}+R_{\mathrm{g} 2}\right)\right]+R_{\mathrm{c} 3} \\ R_{\mathrm{cl}}+R_{\mathrm{gl}} &=0.6366+0.084=0.7206 \times 10^{6} \\ R_{\mathrm{c} 2}+R_{\mathrm{g} 2} &=0.3183+0.085=0.4033 \times 10^{6} \end{aligned}\]
\[\begin{aligned} R_{\mathrm{eq}}&=\left[\dfrac{0.7206 \times 0.4033}{(0.7206+0.4033)}+0.016\right] \times 10^{6}=0.2746 \times 10^{6} \mathrm{AT} / \mathrm{Wb} \\ \phi&=\frac{500}{0.2742 \times 10^{6}}=1823 \mathrm{mWb} \\ B&=\dfrac{1.823 \times 10^{-3}}{50 \times 10^{-4}}=0.365 \mathrm{~T} \\ \phi_{1}&=1.823 \times \dfrac{0.4033}{1.1239}=0.654 \mathrm{mWb} \\ B_{1}&=\dfrac{0.653 \times 10^{-3}}{25 \times 10^{-4}}=0.261 \mathrm{~T} \\ \phi_{2}&=1.823 \times \frac{0.7206}{1.1239}=1.17 \mathrm{mWb} \\ B_{2}&=\dfrac{1.17 \times 10^{-3}}{25 \times 10^{-4}}=0.468 \mathrm{~T} \end{aligned}\]
Problem-7
In the magnetic circuit of Fig., the \(\mu_r\) of the ferromagnetic material is 1200. Neglect magnetic leakage and fringing. All dimensions are in centimetres, and the magnetic material has a square cross-sectional area. Determine the air gap flux, the air gap flux density, and the magnetic held intensity in the air gap.
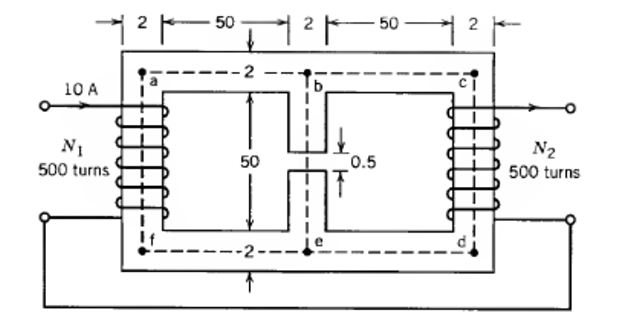
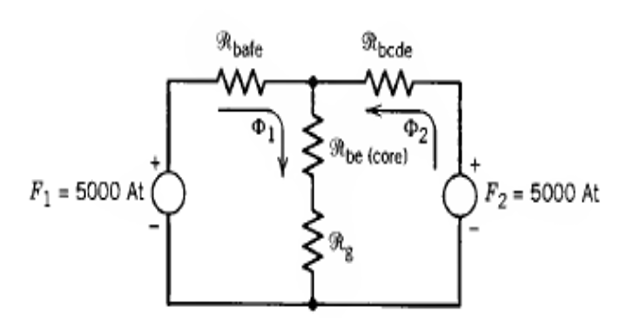
Solution-7
From symmetry: \[\mathscr{R}_{\text {bcde }} =\mathscr{R}_{\text {bafe }}\]
 \[\begin{aligned}
\Re_{g} & =\dfrac{l_{\text{g}}}{\mu_{0}A_{g}}\\
= &
\dfrac{5\times10^{-3}}{4\pi\times10^{-7}\times2\times2\times10^{-4}}\\
= &9.94\times10^{6}~\text{At/Wb}
\end{aligned}\]
\[\begin{aligned}
\Re_{g} & =\dfrac{l_{\text{g}}}{\mu_{0}A_{g}}\\
= &
\dfrac{5\times10^{-3}}{4\pi\times10^{-7}\times2\times2\times10^{-4}}\\
= &9.94\times10^{6}~\text{At/Wb}
\end{aligned}\]
\[\begin{aligned} \Re_{\text{be(core)}} & =\dfrac{l_{\text{be(core)}}}{\mu_{c}A_{c}}\\ = & \dfrac{51.5\times10^{-2}}{1200\times4\pi\times 10^{-7}\times4\times10^{-4}}\\ = & 0.82\times10^{6}~\text{At/Wb} \end{aligned}\]
The loop equations are \[\begin{array}{c} \Phi_{1}\left(\mathscr{R}_{\text {bafe }}+\mathscr{R}_{\mathrm{be}}+\mathscr{R}_{\mathrm{g}}\right)+\Phi_{2}\left(\mathscr{R}_{\mathrm{be}}+\mathscr{R}_{\mathrm{g}}\right)=F_{1} \\ \Phi_{1}\left(\mathscr{R}_{\mathrm{be}}+\mathscr{R}_{\mathrm{g}}\right)+\Phi_{2}\left({R}_{\text {bcde }}+\mathscr{R}_{\mathrm{be}}+\mathscr{R}_{\mathrm{g}}\right)=F_{2} \\ \Phi_{1}\left(13.34 \times 10^{6}\right)+\Phi_{2}\left(10.76 \times 10^{6}\right)=5000 \\ \Phi_{1}\left(10.76 \times 10^{6}\right)+\Phi_{2}\left(13.34 \times 10^{6}\right)=5000 \\ \Phi_{1}=\Phi_{2}=2.067 \times 10^{-4} \mathrm{~Wb} \end{array}\]
The air gap flux is \[\Phi_{\mathrm{g}}=\Phi_{1}+\Phi_{2}=4.134 \times 10^{-4} \mathrm{~Wb}\] The air gap flux density is \[B_{\mathrm{g}}=\frac{\Phi_{\mathrm{g}}}{A_{\mathrm{g}}}=\frac{4.134 \times 10^{-4}}{4 \times 10^{-4}}=1.034 \mathrm{~T}\] The magnetic intensity in the air gap is \[H_{\mathrm{g}}=\frac{B_{\mathrm{g}}}{\mu_{0}}=\frac{1.034}{4 \pi 10^{-7}}=0.822 \times 10^{6} \mathrm{At} / \mathrm{m}\]
Problem-8
A ferromagnetic core with a relative permeability of 1500 is shown in Figure. Because of fringing effect, the effective area of the air gaps is 5% larger than their physical size. Current in the coil is 1 A.
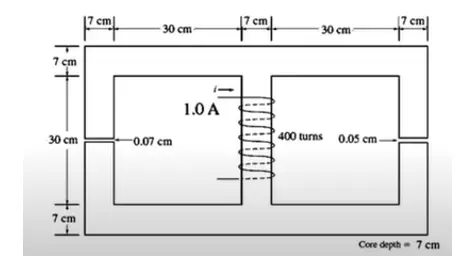
- What is the flux in each of the left, center and right legs of the core.
- What is the flux density in each air gap?
Solution-8
\[ \begin{aligned} & R_{1}=\frac{l_{1}}{\mu_{0}\mu_{r}A_{1}} \\ & l_1=3.5+30+3.5+3.5+30+3.5+3.5+30+3.5=111cm=1.11m \\ & A_{1}=7 \times 7=49 cm^{2}=0.0049m^{2} \\ & \boxed{R_{1} = \frac{1.11}{1500\times4\pi\times10^{-7}\times0.0049}=120.178 \times 10^{3}~\mathrm{At/Wb}} \\ & \text{Air gap in left side:} \\ & R_{g1}=\frac{l_{g1}}{\mu_{0}A_{g1}} \\ & l_{g1}=0.07 cm=0.0007 m \\ & A_{g1}=0.0049\times1.05=0.0051 m^{2} \\ & \boxed{R_{g1} = \frac{0.0007}{4\pi \times10^{-7} \times 0.0051}=109.22 \times 10^{3} ~\mathrm{At/Wb}} \end{aligned} \]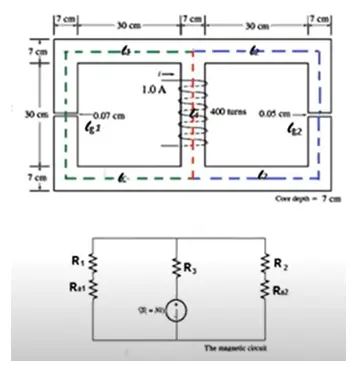 \[
\begin{aligned}
& \boxed{R_{2}= \frac {l_{2}}{\mu _{0}\mu _{r}A_{2}} =120.178 \times 10^{3}~\mathrm{At/Wb}} \\
& \text{Air gap in the Right side:}\\
& R_{g2}=\frac{l_{g2}}{\mu_{0}A_{g2}} \\
& l_{g2}= 0. 05~cm= 0. 0005~m \\
& A_{g2}=0.0049 \times 1.05=0.0051\:m^2 \\
& \boxed{R_{g2}=\frac{0.0005}{4\pi\times10^{-7}\times0.0051}=78.015\times10^{3}~\mathrm{At/Wb}} \\
& l_{3}=3.5+30+3.5=37cm=0.37m \\
& A_3=49\:cm^2=0.0049\:m^2 \\
& \boxed{R_{3}=\frac{l_{3}}{\mu_{0}\mu_{r}A_{3}}=\frac{0.37}{1500\times4\pi\times10^{-7}\times0.0049}=40.6^{*}10^{3}~\mathrm{At/Wb}}\\
\end{aligned}
\]
\[
\begin{aligned}
& \boxed{R_{2}= \frac {l_{2}}{\mu _{0}\mu _{r}A_{2}} =120.178 \times 10^{3}~\mathrm{At/Wb}} \\
& \text{Air gap in the Right side:}\\
& R_{g2}=\frac{l_{g2}}{\mu_{0}A_{g2}} \\
& l_{g2}= 0. 05~cm= 0. 0005~m \\
& A_{g2}=0.0049 \times 1.05=0.0051\:m^2 \\
& \boxed{R_{g2}=\frac{0.0005}{4\pi\times10^{-7}\times0.0051}=78.015\times10^{3}~\mathrm{At/Wb}} \\
& l_{3}=3.5+30+3.5=37cm=0.37m \\
& A_3=49\:cm^2=0.0049\:m^2 \\
& \boxed{R_{3}=\frac{l_{3}}{\mu_{0}\mu_{r}A_{3}}=\frac{0.37}{1500\times4\pi\times10^{-7}\times0.0049}=40.6^{*}10^{3}~\mathrm{At/Wb}}\\
\end{aligned}
\]
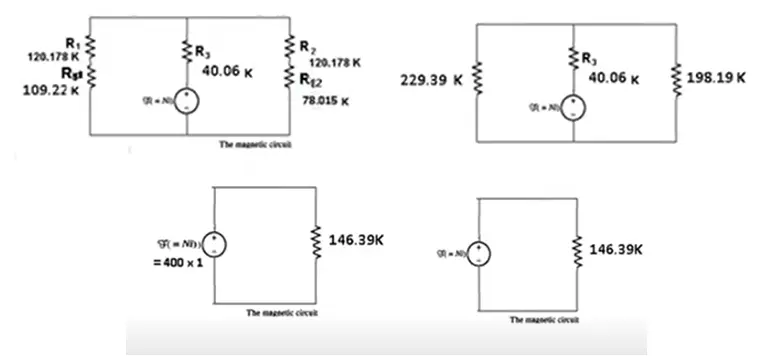 \[
\boxed{\begin{aligned}R_{total}&=( 40.6+229.39 || 198.19 )\times 10^3\\&=( 40.6+106.33)\times 10^3=146.39\times 10^3\end{aligned}}
\]
a.) What is the flux in each of the left, center and right
\[
\begin{aligned}
& \text { Flux }(\phi)=\frac{m \cdot m \cdot f}{R_{\text {total }}}=\frac{400 * 1}{146.39 * 10^3}=0.0027 \mathrm{wb} \\
& \phi_{\text {center }}=0.0027 \mathrm{wb}
\end{aligned}
\]
\[
\begin{aligned}
& \phi_{\text {left }}=\frac{0.0027}{(229.39+198.19) * 10^3} * 198.19 * 10^3=0.0013 \mathrm{wb} \\
& \phi_{\text {right }}=\frac{0.0027}{(229.39+198.19) * 10^3} * 229.39 * 10^3=0.0014 \mathrm{wb}
\end{aligned}
\]
b.) What is the flux density in each air gap?
\[
\begin{aligned}
& B_{\text {leftag }}=\frac{\phi_{\text {left }}}{\mathrm{A}_{g 1}}=\frac{0.0013}{0.0051}=0.2549 \mathrm{~T} \\
& B_{\text {rightag }}=\frac{\phi_{\text {right }}}{\mathrm{A}_{g 2}}=\frac{0.0014}{0.0051}=0.2745 \mathrm{~T}
\end{aligned}
\]
\[
\boxed{\begin{aligned}R_{total}&=( 40.6+229.39 || 198.19 )\times 10^3\\&=( 40.6+106.33)\times 10^3=146.39\times 10^3\end{aligned}}
\]
a.) What is the flux in each of the left, center and right
\[
\begin{aligned}
& \text { Flux }(\phi)=\frac{m \cdot m \cdot f}{R_{\text {total }}}=\frac{400 * 1}{146.39 * 10^3}=0.0027 \mathrm{wb} \\
& \phi_{\text {center }}=0.0027 \mathrm{wb}
\end{aligned}
\]
\[
\begin{aligned}
& \phi_{\text {left }}=\frac{0.0027}{(229.39+198.19) * 10^3} * 198.19 * 10^3=0.0013 \mathrm{wb} \\
& \phi_{\text {right }}=\frac{0.0027}{(229.39+198.19) * 10^3} * 229.39 * 10^3=0.0014 \mathrm{wb}
\end{aligned}
\]
b.) What is the flux density in each air gap?
\[
\begin{aligned}
& B_{\text {leftag }}=\frac{\phi_{\text {left }}}{\mathrm{A}_{g 1}}=\frac{0.0013}{0.0051}=0.2549 \mathrm{~T} \\
& B_{\text {rightag }}=\frac{\phi_{\text {right }}}{\mathrm{A}_{g 2}}=\frac{0.0014}{0.0051}=0.2745 \mathrm{~T}
\end{aligned}
\]