Solved Problems on DC Machines Fundamentals

Demonstrative Video

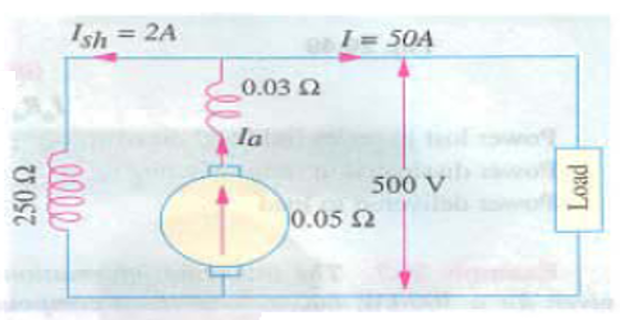
Problem-1

A long-shunt compound generator delivers a load current of 50 A at 500 V and has armature, series field and shunt field resistance of 0.05 \(\Omega\), 0.03 \(\Omega\), and 250 \(\Omega\) respectively. Calculate the generated voltage and the armature current. Allow 1 V per brush for contact drop.

Solution-1

\[\begin{aligned} I_{s h}&=500 / 250=2 \mathrm{~A}\\ I_a & =50+2=52 \mathrm{~A} \end{aligned}\]

\[=52 \times 0.03=1.56 \mathrm{~V}\]

\[\begin{aligned} I_{a} R_{a} &=52 \times 0.05=2.6 \mathrm{~V} \\ \text { Drop at brushes } &=2 \times 1=2 \mathrm{~V} \end{aligned}\]

Series winding Voltage drop

\[=500+2.6+1.56+2=506.16 \mathrm{~V}\]

\(+\)\(E_{g}=V+I_{a} R_{a}+\)

Problem-2

A short-shunt compound generator delivers a load current of 30 A at 220 V and has armature, series field and shunt field resistance of 0.05 \(\Omega\), 0.30 \(\Omega\), and 200 \(\Omega\) respectively. Calculate the induced emf and the armature current. Allow 1 V per brush for contact drop.

Solution-2

\[\begin{aligned} \text{Voltage drop in series winding}&=30 \times 0.3=9 \mathrm{~V} \\ \text{Voltage across shunt winding} &=220+9=229 \mathrm{~V}\\ I_{s h} &=229 / 200=1.145 \mathrm{~A} \\ I_{a} &=30+1.145=31.145 \mathrm{~A} \\ I_{a} R_{a} &=31.145 \times 0.05=1.56 \mathrm{~V} \\ \text { Brush drop } &=2 \times 1=2 \mathrm{~V} \end{aligned}\]

\[\begin{aligned} E_{g} &=V+\text { series drop }+\text { brush drop }+I_{a} R_{a} \\ &=220+9+2+1.56=232.56 \mathrm{~V} \end{aligned}\]

Problem-3

In a long-shunt compound generator, the terminal voltage is 230 V when generator delivers 150 A. Determine

induced emf
total power generated
distribution of this power.

Given the shunt field, series field, divertor and armature resistance are 92 \(\Omega\), 0.015 \(\Omega\), 0.03 \(\Omega\) and 0.032 \(\Omega\) respectively.

Solution-3

\[\begin{aligned} I_{sh} & = 230/92=2.5~\mathrm{A} \\ I_{a} & = 150+2.5=152.5~\mathrm{A} \end{aligned}\]

\[=0.03\times 0.015/0.045=0.01~\Omega\]

Combined resistance of series field and divertor resistance in parallel

Total armature circuit resistance \(=0.032+0.01=0.042~\Omega\)
Voltage drop \(=152.5\times 0.042=6.4~\mathrm{V}\)
Armature voltage \(=E_g=230+6.4=236.4~\mathrm{V}\)
Armature gen. power \(=E_gI_a = 236.4\times 152.5=36051~\mathrm{W}\)
\[\begin{aligned} I_{a}^2 R_{a}&=152.5^{2} \times 0.032=744 \mathrm{~W}\\ \text { series field and divertor }&=152.5^{2} \times 0.01=232 \mathrm{~W}\\ \text {shunt winding } & =V I_{s h}=230 \times 0.01=575 \mathrm{~W} \\ \text { Power delivered to load } & =230 \times 150 =34500 \mathrm{~W}\\ &\text { Total }=36,051 \mathrm{~W} \end{aligned}\]
Armature power loss

Problem-4

The following information is given for a 300-kW, 600 V, long-shunt compound generator: Shunt field resistance = 75 \(\Omega\), armature resistance including brush resistance = 0.03 \(\Omega\), commutating field winding resistance = 0.011 \(\Omega\), series field resistance = 0.012 \(\Omega\), divertor resistance = 0.036 \(\Omega\). When the machine is delivering full load, calculate the voltage and power generated by the armature.

Solution-4

\[\begin{aligned} \text{Power output} & =300,000\mathrm{W}\\ \text{Output current} & =300,000/600 =500\mathrm{A}\\ I_{sh} & =600/75=8\mathrm{A}\\ I_{a} & =500+8=508\mathrm{A} \end{aligned}\]

\[=\dfrac{0.012\times 0.036}{0.048}=0.009~\Omega\]

combined resistance of series field and divertor resistance in parallel

\[=0.03+0.011+0.009=0.05~\Omega\]
Total armature circuit resistance
Voltage drop \(= 508\times 0.05=25.4~\mathrm{V}\)
Voltage generated by armature \(=600+25.4=625.4~\mathrm{V}\)
Power generated \(=625.4\times 508=317700= 317.7~\mathrm{kW}\)

Problem-5

A four-pole generator, having lap-wound armature winding has 51 slots, each slot containing 20 conductors. What will be the voltage generated in the machine when driven at 1500 rpm assuming the flux per pole to be 7 mWb?

Solution-5

\[\begin{aligned} Z & =51\times20=1020\\ A & =P=4\\ E_{g} & =\dfrac{\phi PN}{60}\times\dfrac{Z}{A}\\ & =\dfrac{7\times10^{-3}\times4\times1500}{60}\times\dfrac{1020}{4}\\ & =178.5\mathrm{V} \end{aligned}\]

Problem-6

An 8-pole dc generator has 500 armature conductors, and a useful flux of 0.05 Wb per pole. What will be the emf generated if it is lap-connected and runs at 1200 rpm? What must be the speed at which it is to be driven producing the same emf if its is wave-wound?

Solution-6

With Lap-winding:

\[\begin{aligned} P&=A=8\\ E & =\dfrac{\phi PN}{60}\times\dfrac{Z}{A}\\ & =\dfrac{0.05\times8\times1200}{60}\times\dfrac{500}{8}\\ & =500~\mathrm{V} \end{aligned}\]
\[\begin{aligned} E & =\dfrac{0.05\times8\times N}{60}\times\dfrac{500}{2}\\ \rightarrow500 & =\dfrac{5N}{3}\\ \Rightarrow N & =300~\text{rpm} \end{aligned}\]
If wave winding:

Problem-7

A 4-pole dc motor is lap-wound with 500 conductors. The pole shoe is 25 cm long and average flux density over one-pole-pitch is 0.5 T, the armature diameter being 30 cm. The motor runs at a speed of 1500 rpm.

Determine:

flux per pole
Induced emf

Solution-7

Note:

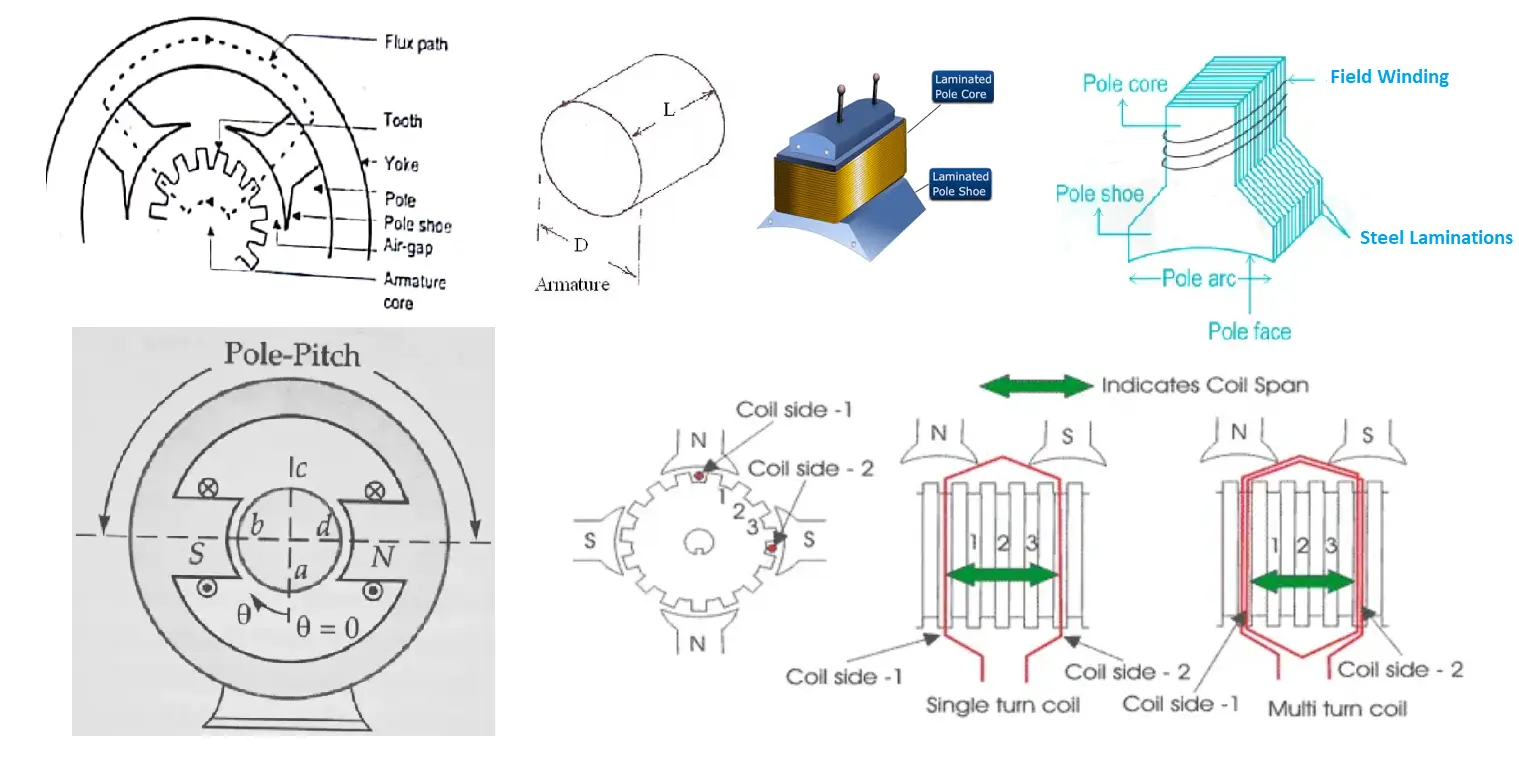
Pole pitch:
distance between the centers of two adjacent poles in a DC machine.
It is measured in terms of armature slots or conductors, or on the circumference of the armature.
In an electrical machine, the pole pitch is also equal to 180° electrical.
The pole pitch can be calculated by dividing the total number of armature slots by the number of poles in the machine.
For example, if there are 80 conductors and 8 poles, the pole pitch would be 10 (80/8).

\[ \begin{aligned} \phi & = \text{Average flux/pole} \\ P & = \text{No. of poles} \\ \text{Total flux called the magnetic loading} & = P\phi \end{aligned} \]

Magnetic loading/unit area of the armature surface is called the specific magnetic loading or average value of the flux density in the air gap}, \(B_{avg.}\)

\[ \boxed{B_{avg.} = \dfrac{P\phi}{\pi \cdot D \cdot L}} \] \[ \begin{aligned} & Flux/_{pole}=\frac{\pi\times30\times10^{-2}}4\times25\times0.5\times10^{-2}=\boxed{0.0294wb}\\&\text{Induced EMF}=\frac{\Phi nZ}{60}\left(\frac PA\right)\\ &=\frac{0.0294\times1500\times500}{60}\left(\frac44\right)=\boxed{367.5\text{ Volt}}\end{aligned} \]

Problem-8

A wave connected armature winding has 19 slots with 54 conductors per slot. If the flux per pole is 0.025 Wb and number of poles is 8, find the speed at which the generator should be run to give 513 V. Also find the speed if the armature is lap connected.

Solution-8

\[ \begin{aligned} & \mathrm{P}=8 \\ & \varphi=0.025 \mathrm{~Wb} \\ & \mathrm{Z}=19 \times 54=1026 \\ & \mathrm{~A}=2 \text { (for wave) } \\ & \mathrm{E}_{\mathrm{g}}=513 \text { Volts } \end{aligned} \] \[\mathrm{EMF~(E_g)}=\frac{\Phi nZ}{60}\left(\frac PA\right)\] \[\begin{aligned}&\mathrm{n}= \frac{60\mathrm{E}_{\mathrm{g}}A}{\Phi ZP} =\frac{60\times513\times2}{0.025\times1026\times8}=300 \mathrm{rpm} ( \mathrm{For~wave~wound~A=2})\\&\mathrm{n}=\frac{60\times513\times8}{0.025\times1026\times8}=1200 \mathrm{rpm}\quad( \mathrm{For~lap~wound~A=P})\end{aligned}\]

Problem-9

In a DC machine, with the number of poles being equal to 4, find the relation between electrical angle and mechanical angle.
For a DC machine, if electrical degree is twice as mechanical degrees, then find the number of pole pairs.

Solution-9

The relation between electrical and mechanical angle,

\[ \text{Electrical angle}=\dfrac{P}{2} \text{(mechanical angle)}. \]

First-part

Given

Second part

Problem-10

Calculate the Pole Pitch for a 4-pole DC machine with single-turn 12 coil 2-layer winding. If the same machine winding is made 2/3rd of full-pitch then calculate the electrical angle of the coil span and mechanical angle.

Solution-10

Pole Pitch \(=\dfrac{12 \times 2}{4}=6\)
For \(2 / 3^{\text {rd }}\) of the Full-pitch coil span,

Electrical angle of coil span \(=180^{\circ} \times \dfrac{2}{3}=120^{\circ}\)
At this condition the Mechanical angle \(=\dfrac{2 \times 120}{4}=60^{\circ}\)