Master Inductor Connections: Inductances in Series and Parallel

Inductances in Series and Parallel

• Consider two coils magnetically coupled having self-inductance of \(L_1\) and \(L_2\) respectively, and a mutual-inductance of \(M\) henry.

• The two coils, in an electrical circuit, may be connected in different ways giving different values of resultant inductance.

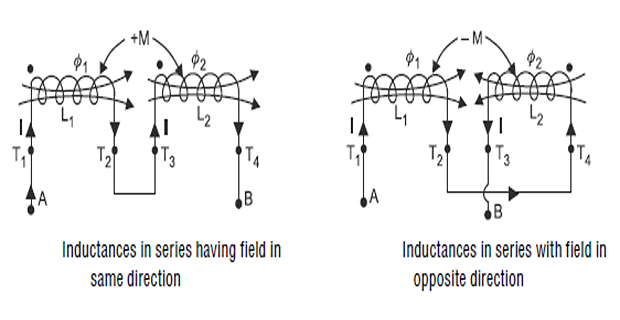
Inductances in Series

The two coils may be connected in series in the following two ways:

1. When their fields (or mmfs.) are additive i.e., their fluxes are set-up in the same direction. In this case, the inductance of each coil is increased by \(M\) i.e., Total inductance, \(L_{T}=\left(L_{1}+M\right)+\left(L_{2}+M\right)=L_{1}+L_{2}+2 M\)

2. When their fields (or mmfs.) are subtractive i.e., their fluxes are set-up in opposite direction. s In this case, the inductance of each coil is decreased by \(M\), i.e. Total inductance, \(L_{T}=\left(L_{1}-M\right)+\left(L_{2}-M\right)=L_{1}+L_{2}-2 \mathrm{M}\)

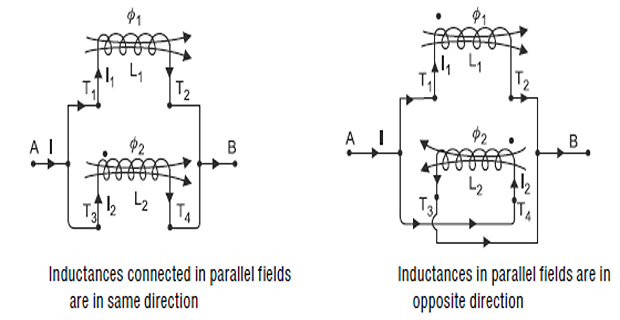
Inductances in Parallel

The two coils may be connected in parallel in the following two ways:

1. When the fields (or mmfs.) produced by them are in the same direction Total inductance, \(L_{T}=\frac{L_{1} L_{2}-M^{2}}{L_{1}+L_{2}-2 M}\)

2. When the fields (or mmfs.) produced by them are in the opposite direction Total inductance, \(L_{T}=\frac{L_{1} L_{2}-M^{2}}{L_{1}+L_{2}+2 M}\)

Energy Stored in a Magnetic Field

• When some electrical energy is supplied to a coil, it is spent in two ways:

  1. A part of it is spent to meet \(I^2R\) loss which is dissipated in the form of heat and cannot be recovered.

  2. The remaining part is used to create magnetic field around the coil and is stored in the magnetic field. When this field collapses, the stored energy is released by the coil and is returned to the circuit.

• The energy stored in the magnetic field is given by the expression: \[\text{Energy stored in magnetic field} = \dfrac{1}{2}LI^2\]