Long Transmission Lines

Demonstrative Video

Revision of Important Formulas

\[\begin{aligned} V_{x}&=\left(\dfrac{V_{R}+I_{R} Z_{C}}{2}\right) e^{\gamma x}+\left(\dfrac{V_{R}-I_{R} Z_{c}}{2}\right) e^{-\gamma x} \\ I_{x}&=\left(\dfrac{V_{R} / Z_{c}+I_{R}}{2}\right) e^{\gamma x}+\left(\dfrac{V_{R} / Z_{c}-I_{R}}{2}\right) e^{-\gamma x} \end{aligned}\]

\[\begin{aligned} V_{x}&=V_{R}\left(\frac{e^{\gamma x}+e^{-\gamma x}}{2}\right)+I_{R} Z_{c}\left(\frac{e^{\gamma x}-e^{-\gamma x}}{2}\right)\\ &=V_{R} \cosh (\gamma x)+I_{R} Z_{c} \sinh (\gamma x) \\ I_{x}&=V_{R} \frac{1}{Z_{c}}\left(\frac{e^{\gamma x}-e^{-\gamma x}}{2}\right) e^{\gamma x}+I_{R}\left(\frac{e^{\gamma x}+e^{-\gamma x}}{2}\right)\\ &=I_{R} \cosh (\gamma x)+V_{R} \frac{1}{Z_{c}} \sinh (\gamma x) \end{aligned}\]

when \(x = l, \quad V_{x} = V_{s}, \quad I_{x} = I_{s}\)

\[ \boxed{ \left[\begin{array}{c} V_S \\ I_S \end{array}\right]=\left[\begin{array}{cc} \cosh (\gamma l) & Z_c \sinh (\gamma l) \\ \frac{1}{Z_c} \sinh (\gamma l) & \cosh (\gamma l) \end{array}\right]\left[\begin{array}{c} V_R \\ I_R \end{array}\right] } \]

\[\begin{aligned} V_{x}&=\left|\frac{V_{R}+I_{R} Z_{c}}{2}\right| e^{\alpha x} e^{j\left(\beta x+\phi_{1}\right)}+\left|\frac{V_{R}-I_{R} Z_{c}}{2}\right| e^{-\alpha x} e^{-j\left(\beta x-\phi_{2}\right)} \end{aligned}\]

where

\[\begin{aligned} &\boxed{Z_{c}=\sqrt{\left(\dfrac{z}{y}\right)}} \\ &\boxed{\gamma=\sqrt{y z}} \\ \gamma&=\sqrt{y z}=\boxed{\alpha+j \beta} \end{aligned}\]

\[\begin{aligned} \boxed{\cosh (\alpha l+j \beta l)} & =\cosh (\alpha l) \cos (\beta l)+j \sinh (\alpha l) \sin (\beta l) \\ \boxed{\sinh (\alpha l+j \beta l)}& =\sinh (\alpha l) \cos (\beta l)+j \cosh (\alpha l) \sin (\beta l) \end{aligned}\]

Problem

\[R = 0.2~ \Omega, ~ L = 1.3~\text{mH}, ~ \text{and}~ C = 0.01~\mu F\]

TL has the following parameters per km: A single circuit 50 Hz, 3-

The incident voltage to neutral at the receiving end (reference)
The reflected voltage to neutral at the receiving end
The incident and reflected voltage to neutral at 120 km from the receiving end

Also,

Determine the efficiency of the line, if the line is 120 km long and delivers 40 MW at 132 kV and 0.8 pf lagging
Determine the ABCD parameters of the line
Determine the sending end voltage and efficiency using nominal-\(\pi\) and nominal-T methods.

Solution

\[\begin{aligned} z &=r+j x=\left(0.2+j 1.3 \times 314 \times 10^{-3}\right)=(0.2+j 0.408) \\ &=0.454 \angle 63.88^{\circ} \end{aligned}\]
The series impedance per unit length of the line
\[=3.14 \times 10^{-6} \angle+90^{\circ}\]
The shunt admittance
The characteristic impedance \(Z_{c}=\sqrt{\dfrac{z}{y}}=\sqrt{\dfrac{0.454}{0.314} \times 10^{5} \angle 63.88-90^{\circ}} =380 \angle-13.06^{\circ}\)

\[\begin{array}{l} \gamma=\sqrt{y z}=\sqrt{0.314 \times 0.454 \times 10^{-6}} \angle(90+63.88)^{\circ} / 2 \\ =(0.2714+j 1.169) \times 10^{-3} \\ =(\alpha+j \beta) \end{array}\]
Propagation constant:
\[=\frac{132 \times 1000}{\sqrt{3}}=76200 \text { volts }\]
The receiving end line to neutral voltage
\[I_{r}=0\]
The receiving end current under open circuited condition

\[=\frac{V_{r}+I_{r} Z_{c}}{2}\]
\[\text { Incident voltage }=\frac{V_{r}}{2}=\frac{76200}{2}=38100 \text { volts }\]
\(I_{r}=0\) Incident voltage to neutral at the receiving end
\[\frac{V_{r}-I_{r} Z_{c}}{2}=\frac{V_{r}}{2}=38100 \mathrm{volts}\]
Reflected voltage to neutral at the receiving end

\[\begin{aligned} V_{r}^{+} &=V_{r} \exp (\alpha x) \exp (j \beta x) \\ &=76.2 \exp \left(0.2714 \times 120 \times 10^{-9}\right) \exp \left(j 1.169 \times 120 \times 10^{-3}\right) \\ &=78.7 \angle 8.02^{\circ} \\ V_{r}^{-} &=76.2 \exp (-\alpha x) \exp (-j \beta x)\\ &=76.2 \exp (-0.0325) \exp (-j 0.140) \\ &=73.76 \angle-8.02^{\circ} \end{aligned}\]
from the receiving end At a distance of
\[=\frac{73.76}{2} \angle-8.02^{\circ}=36.88 \angle-8.02^{\circ} \mathrm{kV}\]
from the receiving end Reflected voltage at a distance of
\[=\frac{78.7}{2} \angle 8.02^{\circ}=39.35 \angle 8.02^{\circ}\]
from the receiving end Incident voltage at a distance of

\[\begin{aligned} I_{r} &=\frac{40 \times 1000}{\sqrt{3} \times 132 \times 0.8} \\ &=218.7 \text { amps. } \end{aligned}\]
Receiving end current
\[Z_{c}=380 \angle-13.06^{\circ}\]
Characteristics impedance
\[\begin{aligned} e^{\alpha x} e^{j \beta x} &=1.033 \angle 8.02^{\circ} \\ e^{-\alpha x} e^{-j \beta x} &=0.968 \angle-8.02^{\circ} \end{aligned}\]
length of line, and For

\[\begin{aligned} I_{r} &=218.7 \angle-36.8^{\circ} \\ V_{s}^{+} &=\frac{V_{r}+I_{r} Z_{c}}{2} e^{\alpha x} e^{j \beta x} \\ &=\frac{76200+380 \times 218.7 \angle-13.06 \angle-36.8}{2} \times 1.033 \angle 8.02^{\circ} \\ &=74.63 \angle-18^{\circ} \\ V_{s}^{-} &=\frac{V_{r}-I_{r} Z_{c}}{2} e^{-\alpha x} e^{-j \beta x} \\ &=\frac{76200-380 \times 218.7 \angle-49.86}{2} \times 0.968 \angle-8.02^{\circ} \\ &=32.619 \angle 62.37 \mathrm{kV} \\ V_{s} &=V_{s}^{+}+V_{s}^{-}=74.63 \angle-18^{\circ}+32.619 \angle 62.37^{\circ} \\ &=86077+j 5751=86.26 \angle 3.82^{\circ} \end{aligned}\]

as the reference, Taking

\[\begin{aligned} I_{s} &=\frac{V_{r} / Z_{c}+I_{r}}{2} e^{\alpha x} e^{j \beta x}-\frac{V_{r} / Z_{c}-I_{r}}{2} e^{-\alpha x} e^{-j \beta x} \\ &=\frac{V_{s}^{+}}{Z_{c}}-\frac{V_{s}^{-}}{Z_{c}}\\ &=\left(\frac{74.63 \angle-18^{\circ}}{380 \angle-13.06^{\circ}}-\frac{32.619 \angle 62.37^{\circ}}{380 \angle-13.06^{\circ}}\right) \mathrm{kA} \\ &=200.39 \angle-29.9^{\circ} \end{aligned}\]

Efficiency

\[\begin{aligned} &=3 \times\left|V_{s}\right|\left|I_{s}\right| \cos \phi_{s} \\ &=3 \times 86.26 \times 200.39 \mathrm{cos} 33.72 \\ &=43.132 ~\mathrm{MW} \end{aligned}\]
Power at the sending end
\[\% \eta =\dfrac{40}{43.132} \times 100=92.7 \%\]
Efficiency

ABCD parameters

\[\begin{aligned} & \gamma l=(0.2714+j 1.169) 120 \times 10^{-3}\\ &=0.03254+j 0.1402 \end{aligned}\]

\[\begin{aligned} A = D &=\cosh \gamma l\\ &=\cosh (0.03254+j 0.1402) \\ &=\cosh 0.03254 \cos 0.1402+j \sinh 0.03254 \sin 0.1402 \\ &=0.99+j 0.004435=0.99 \angle 0.26^{\circ} \end{aligned}\]

\[\begin{aligned} \sinh \gamma l &=\sinh \alpha l \cos \beta l+j \cosh \alpha l \sin \beta l \\ &=\sinh 0.03254 \cos 0.1402+j \cosh 0.03254 \sin 0.1402 \\ &=0.031958+j 0.1386 \\ &=0.1422 \angle 77^{\circ} \end{aligned}\]

\[\begin{aligned} B &=Z_{c} \cdot \sinh \gamma l=380 \angle-13.06^{\circ} \times 0.1422 \angle 77^{\circ} \\ &=54.03 \angle 64^{\circ} \end{aligned}\]

\[\begin{aligned} C &=\dfrac{1}{Z_{c}} \cdot \sinh \gamma l\\ & =\dfrac{1}{380 \angle-13.06^{\circ}} \times 0.1422 \angle 77^{\circ} \\ &=3.74\times 10^{-4} \angle 90.06^{\circ} \end{aligned}\]

\[\begin{aligned} V_{s} &=A V_{r}+B I_{r} \\ &=0.99 \angle 0.26 \times 76200+54.03 \angle 64^{\circ} \times 218.7 \angle-36.8^{\circ} \\ &=75438+11772 \angle 27.2^{\circ} \\ &=85908+j 5380 \\ &=86.07 \angle 3.588^{\circ} \end{aligned}\]

Nominal-\(\pi\)

The resistance of the line \(=0.2 \times 120=24\) ohms
The inductive reactance \(=1.3 \times 10^{-3} \times 120 \times 314=48.98 \Omega\)
The capacitance \(\quad=0.01 \times 10^{-6} \times 120=1.2 \mu \mathrm{F}\)

The nominal- \(\pi\) circuit will be

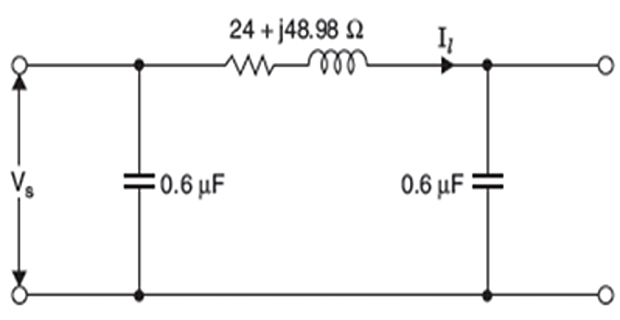
\[\begin{aligned} I_{r} &=218.7(0.8-j 0.6)=174.96-j 131.22 \\ I_{c_{1}} &=j 314 \times 0.6 \times 10^{-6} \times 76200=j 14.356 \mathrm{amp} \\ I_{l} &=I_{c_{1}}+I_{r}=174.96-j 116.86=210.39 \angle 33.73^{\circ}\\ V_{s} &=76200+(174.96-j 116.86)(24+j 48.38) \\ &=76200+4199+j 8596-j 2804+5723 \\ &=86122+j 5765 \\ &=86314 \angle 3.82^{\circ} \mathrm{volts} \\ \text { The loss } &=3 \times 210.39^{2} \times 24=3.187 \mathrm{MW} \\ \% \eta &=\frac{40 \times 100}{43.187}=92.69 \% \end{aligned}\]

Taking receiving end voltage as reference,

Nominal-T

\[\begin{aligned} V_{c} &=76200(0.8+j 0.6)+218.7(12+j 24.49) \\ &=60960+j 45720+2624+j 5356 \\ &=63584+j 51076 \\ I_{c} &=j 314 \times 1.2 \times 10^{-6}(63584+j 51076) \\ &=j 23.95-19.24 \\ I_{s} &=218.7+j 23.95-19.24=199.46+j 23.95 \\ &=200.89 \angle 6.8^{\circ} \\ V_{s} &=63584+j 51076+(199.46+j 23.95)(12+j 24.49) \\ &=63584+j 51076+2393+j 4884.7+j 287.4-586.5 \\ &=65390+j 56248 \\ &=86.25 \angle 40.70^{\circ} \\ \text { The loss }&=3 \times 12\left(200.89^{2}+218.7^{2}\right)\\ &=3.174~ \mathrm{MW} \\ \% \eta & =\frac{40}{43.174} \times 100\\ &=92.64 \% \end{aligned}\]

Taking receiving end current as reference