Power in Three-Phase Circuits
Demonstrative Video
Lecture-3: Overview
\(1-\phi\) and \(3-\phi\) Circuits & Quantities
Voltages and Currents in \(Y\) and \(\Delta\) Connections
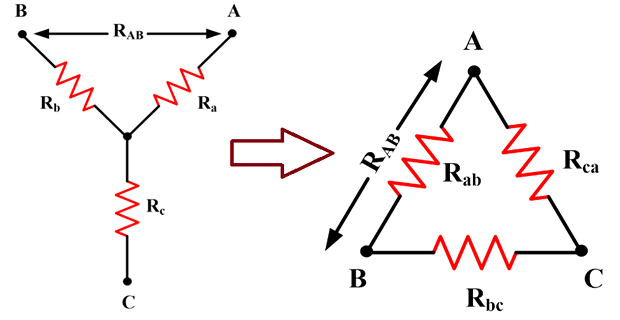
\(Y \leftrightarrow \Delta\) conversion
Power in \(3-\phi\) circuits
\(3-\phi\) Circuits
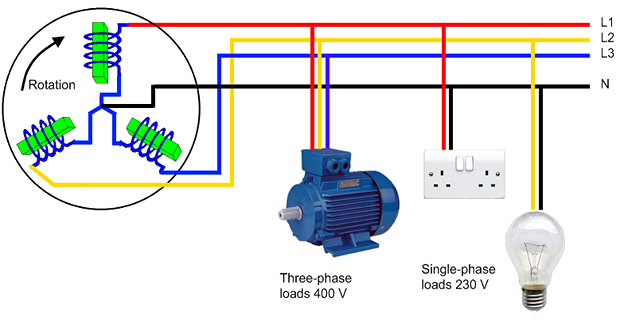
Mostly electricity is generated by \(3-\phi\) AC generators
\(3-\phi\) system
has three phases, i.e., the current will pass through the three wires
there will be one neutral wire for passing the fault current to the earth ( \(3-\phi\) 4-wire system)
\(3-\phi\) system can be used as a \(1-\phi\) if one of their phase and the neutral wire is taken out from it
C.S.A of the neutral conductor is half of the live wire.
\(1-\phi\) System
\(3-\phi\) System
Why \(3-\phi\) is Preferred Over \(1-\phi\)?
Advantages of \(3-\phi\) over \(1-\phi\) system:
can be used as 3 \(\times\) \(1-\phi\) system
conductor needed is 75% of \(1-\phi\) circuit
instantaneous power in \(1-\phi\) system falls down to zero as can seen from the sinusoidal curve but in \(3-\phi\) the net power from all the phases gives a continuous power to the load.
higher efficiency and minimum losses
Phase Sequence, Line and Phase Quantities
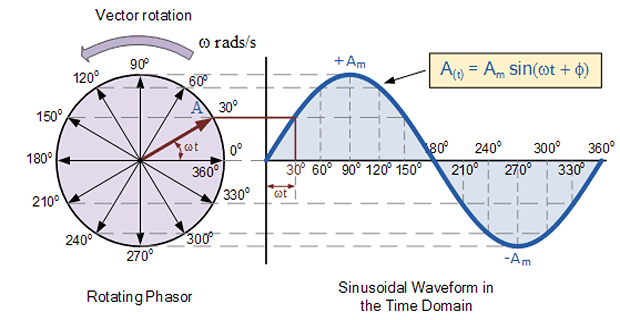
Sinusoidal steady state and balanced condition \(\rightarrow\) 3-voltages are equal in magnitude and displaced by \(120^{\circ}\) w.r.t each other
Phase sequence: of voltage \(a-b-c\), where \(a\)-phase leads \(b\) by \(120^{\circ}\), \(b\) leads \(c\) by \(120^{\circ}\) and so on
Phase sequence applies to both time-domain and phasor-domain
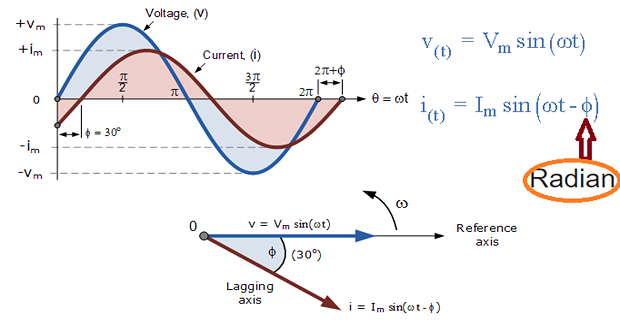
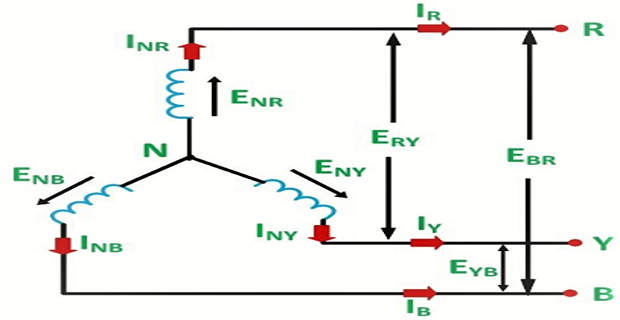
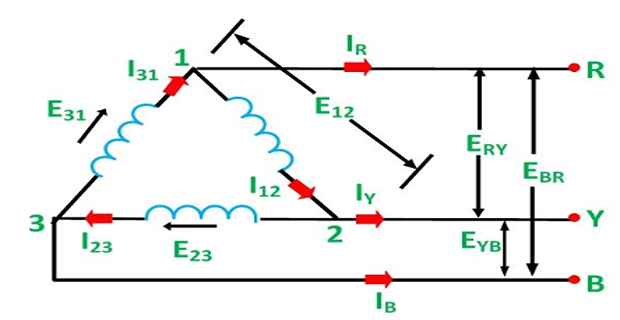
Line Voltage: measured between any two line conductors
Phase Voltage: measured across any one component (source winding or load impedance)
Line current through any one line between a three-phase source and load
Phase current through any one component comprising a three-phase source or load.
\(3-\phi\) AC circuits are either \(Y\) or \(\Delta\) connected
Line/Phase and Load in \(3-\phi\) System
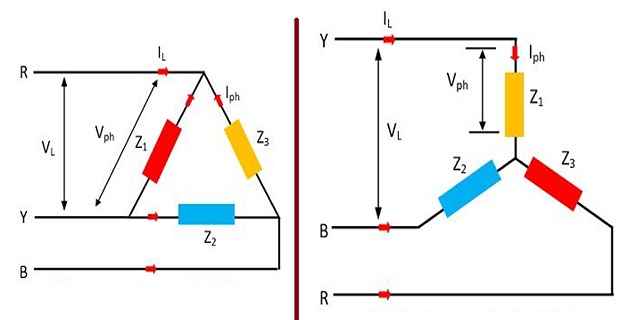
STAR (Y): Current & Voltage Relations
\[
\begin{aligned}
&\mathrm{E}_{\mathrm{NR}}=\mathrm{E}_{\mathrm{NY}}=\mathrm{E}_{\mathrm{NB}}=\mathrm{E}_{\mathrm{ph}}(\text{ in mag.})\\
&\overline{\mathrm{E}_{\mathrm{NR}}}+\overline{\mathrm{E}_{\mathrm{RY}}}-\overline{\mathrm{E}_{\mathrm{NY}}}=0\\
\Rightarrow&\overline{\mathrm{E}_{\mathrm{RY}}}=\overline{\mathrm{E}_{\mathrm{NY}}}-\overline{\mathrm{E}_{\mathrm{NR}}}(\text { vector diff.}) \\
\mathrm{E}_{\mathrm{RY}}& =\sqrt{\mathrm{E}_{\mathrm{NY}}^{2}+\mathrm{E}_{\mathrm{NR}}^{2}+2 \mathrm{E}_{\mathrm{NY}} \mathrm{E}_{\mathrm{NR}} \cos 60^{\circ}}\\
\Rightarrow & E_{L}=\sqrt{E_{p h}^{2}+E_{p h}^{2}+2 E_{p h} E_{p h} \times 0.5 }\\
\Rightarrow&\mathrm{E}_{\mathrm{L}}=\sqrt{3 \mathrm{E}_{\mathrm{ph}}^{2}}=\sqrt{3} \mathrm{E}_{\mathrm{ph}} \text { (in mag.) }
\\
&\mathrm{I}_{\mathrm{NR}}=\mathrm{I}_{\mathrm{NY}}=\mathrm{I}_{\mathrm{NB}}=\mathrm{I}_{\mathrm{ph}} \\
&\mathrm{I}_{\mathrm{R}}=\mathrm{I}_{\mathrm{Y}}=\mathrm{I}_{\mathrm{B}}=\mathrm{I}_{\mathrm{L}}
\end{aligned}
\]
Delta(\(\Delta\)): Current & Voltage Relations
\[
\begin{aligned}
&\mathrm{E}_{12}=\mathrm{E}_{\mathrm{RY}};~\mathrm{E}_{23}=\mathrm{E}_{\mathrm{YB}};~ \mathrm{E}_{31}=\mathrm{E}_{\mathrm{BR}} \\
&\mathrm{E}_{12}=\mathrm{E}_{23}=\mathrm{E}_{31}=\mathrm{E}_{\mathrm{ph}} \\
&\mathrm{E}_{\mathrm{RY}}=\mathrm{E}_{\mathrm{YB}}=\mathrm{E}_{\mathrm{BR}}=\mathrm{E}_{\mathrm{L}}
\\
&\mathrm{I}_{12}=\mathrm{I}_{23}=\mathrm{I}_{31}=\mathrm{I}_{\mathrm{ph}} \\
& \overline{\mathrm{I}_{31}}=\overline{\mathrm{I}_{\mathrm{R}}}+\overrightarrow{\mathrm{I}_{12}} \Rightarrow \overline{\mathrm{I}_{\mathrm{R}}}=\overline{\mathrm{I}_{31}}-\overline{\mathrm{I}_{12}} \\
& \mathrm{I}_{\mathrm{R}}=\sqrt{\mathrm{I}_{31}^{2}+\mathrm{I}_{12}^{2}+2 \mathrm{I}_{31} \mathrm{I}_{12} \cos 60^{\circ}} \\
& \mathrm{I}_{\mathrm{L}}=\sqrt{\mathrm{I}_{\mathrm{ph}}^{2}+\mathrm{I}_{\mathrm{ph}}^{2}+2 \mathrm{I}_{\mathrm{ph}} \mathrm{I}_{\mathrm{ph}} \times 0.5} \\
& \mathrm{I}_{\mathrm{L}}=\sqrt{3 \mathrm{I}_{\mathrm{ph}}^{2}}=\sqrt{3} \mathrm{I}_{\mathrm{ph}}
\end{aligned}
\]
\(Y \leftrightarrow \Delta\) Transformation
\[\begin{aligned} R_{a b} &=\frac{R_{a} R_{b}+R_{a} R_{c}+R_{b} R_{c}}{R_{c}} \\ R_{a c} &=\frac{R_{a} R_{b}+R_{a} R_{c}+R_{b} R_{c}}{R_{b}} \\ R_{b c} &=\frac{R_{a} R_{b}+R_{a} R_{c}+R_{b} R_{c}}{R_{a}} \end{aligned}\] \[\begin{aligned} R_{a}& =\frac{R_{a b} R_{a c}}{R_{a b}+R_{a c}+R_{b c}} \\ R_{b}& =\frac{R_{a b} R_{b c}}{R_{a b}+R_{a c}+R_{b c}} \\ R_{c}& =\frac{R_{a c} R_{b c}}{R_{a b}+R_{a c}+R_{b c}} \end{aligned}\]
Power in 1-\(\phi\) and 3-\(\phi\) Circuits
1-\(\phi\) power equation \[\mathrm{P}=\mathrm{VI} \cos \varphi\]
3-\(\phi\) power equation \[\mathrm{P_{3\phi}}=3\mathrm{V_{ph}}\mathrm{I_{ph}} \cos \varphi\]
\(3-\phi\) Y-power \[\begin{aligned} &P=3 \frac{V_{L}}{\sqrt{3}} I_{L} \operatorname{Cos} \varphi \\ \Rightarrow & \mathrm{P}=\sqrt{3} \mathrm{V}_{\mathrm{L}} \mathrm{I}_{\mathrm{L}} \operatorname{Cos} \varphi \end{aligned}\]
\(3-\phi\) \(\Delta\) - power \[\begin{aligned} &\mathrm{P}=3 \mathrm{V}_{\mathrm{L}} \frac{\mathrm{I}_{\mathrm{L}}}{\sqrt{3}} \operatorname{Cos} \varphi\\ \Rightarrow & \sqrt{3} \mathrm{V}_{\mathrm{L}} \mathrm{I}_{\mathrm{L}} \cos \phi \end{aligned}\]
Apparent Power \[\mathrm{P}_{\mathrm{a}}=\sqrt{3} \mathrm{V}_{\mathrm{L}} \mathrm{I}_{\mathrm{L}}\]
Reactive Power \[P_{r}=\sqrt{3} V_{L} I_{L} \sin \varphi\]