Demonstrative Video
Medium Transmission line
TL length of more than 80 kms but less than 250 kms
The parameters (Resistance, Inductance, and Capacitance) are distributed uniformly along the line.
Unlike a short transmission line, the line \(I_c\) of a medium transmission line is appreciable and hence the shunt capacitance must be considered (this is also the case for long transmission lines).
\(Y\) and \(Z\) are considered as a lumped parameter
Lumped parameters can be represented using two different models, namely:
Nominal \(\Pi\) representation (nominal pi model)
Nominal \(\mathrm{T}\) representation (nominal T model)
Nominal \(\mathrm{T}\) representation
\[\begin{aligned}
V_{c} & =V_{r}+I_{r}\left(Z/2\right)\\
I_{S} & =I_{r}+V_{c}Y\\
&=I_{r}+Y \cdot V_{r}+I_{r}\left(Z/2\right)\cdot Y\\
V_{s} & =V_{c}+I_{s}\left(Z/2\right)
\end{aligned}\]
voltage across the
capacitor and Let,
\[V_{s}=V_{r}\left(1+\dfrac{YZ}{2}\right)+I_{r}Z\left(1+\dfrac{YZ}{4}\right)\]
in and Substituting
$$\boxed{
\left[\begin{array}{c}
V_s \\
I_s
\end{array}\right]=\left[\begin{array}{cc}
\left(1+\frac{Y Z}{2}\right) & Z\left(1+\frac{Y Z}{4}\right) \\
Y & \left(1+\frac{Y Z}{2}\right)
\end{array}\right]\left[\begin{array}{c}
V_r \\
I_r
\end{array}\right]
}$$
\[\begin{aligned}
A & = \left(1+\dfrac{YZ}{2}\right) &
B & = Z\left(1+\dfrac{YZ}{4}\right)\\
C & = Y &
D & = \left(1+\dfrac{YZ}{2}\right)
\end{aligned}\]
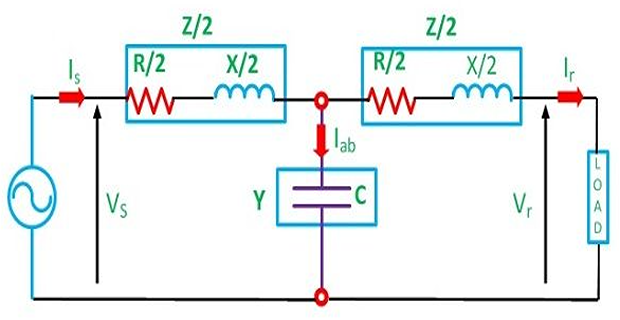
Nominal \(\mathrm{Pi}\) representation
\[\begin{aligned}
I_{s} & =I_{r}+V_{r}\dfrac{Y}{2}+V_{s}\dfrac{Y}{2}\\
V_{s} & =V_{r}+\left(I_{r}+V_{r}\dfrac{Y}{2}\right)Z\\
&=V_{r}\left(1+\dfrac{YZ}{2}\right)+I_{r}Z
\end{aligned}\]
\(\therefore I_{s}=V_{r}Y\left(1+\dfrac{YZ}{4}\right)+I_{r}\left(1+\dfrac{YZ}{2}\right)\)
Hence,
$$\boxed{
\left[\begin{array}{c}
V_s \\
I_s
\end{array}\right]=\left[\begin{array}{cc}
\left(1+\frac{Y Z}{2}\right) & Z \\
Y\left(1+\frac{Y Z}{4}\right) & \left(1+\frac{Y Z}{2}\right)
\end{array}\right]\left[\begin{array}{c}
V_r \\
I_r
\end{array}\right]
}$$
\[\begin{aligned}
A& = \left(1+\dfrac{YZ}{2}\right) &
B& = Z\\
C & =Y\left(1+\dfrac{YZ}{4}\right) &
D & = \left(1+\dfrac{YZ}{2}\right)\\
\end{aligned}\]