Review of Fundamental Concepts of Power Systems

Demonstrative Video

Lecture-2: Overview

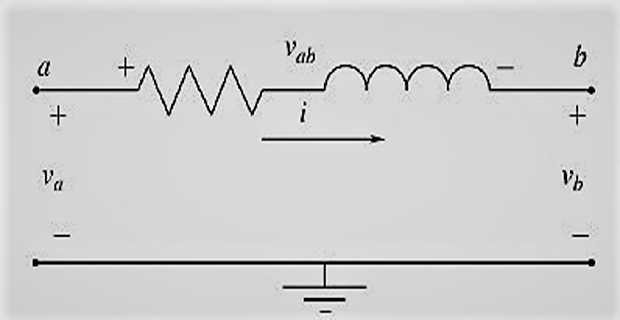
Sign Convention of \(V\) and \(I\)
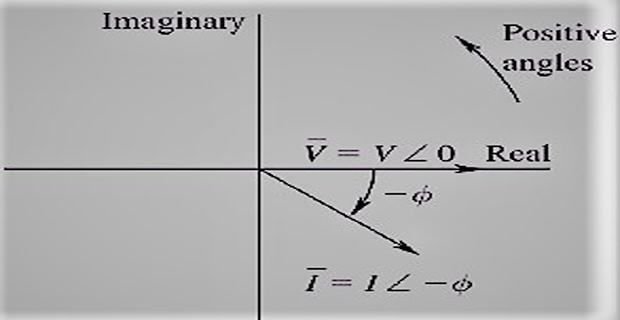
Phasor Representation
Conversion of Time-domain to Phasor and Impedance Triangle
Powers: Instantaneous, Active, Reactive, and Complex
Relationship between the power quantities
Power Factor and its Significance
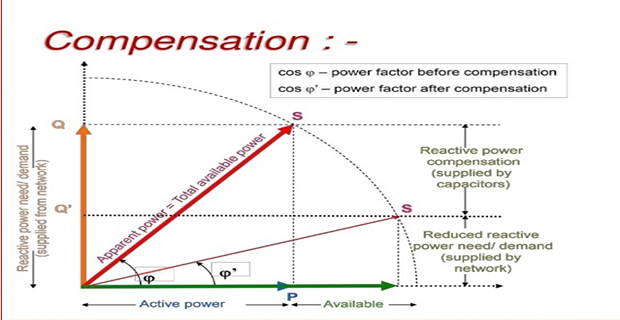
Advantage of Reactive Power Compensation

Sinusoidal \(V\) and \(I\) in Steady State

Convention for \(V\) and \(I\)

In linear circuit with sinusoidal \(V\) and \(I\) of frequency \(f\) applied for long so that steady state is reached, all \(V\) and \(I\) are at \(f=\omega/2\pi\)
Phasor converts \(v(t)\) and \(i(t)\) to complex variables \(\overrightarrow{V}\) and \(\overrightarrow{I}\)

Phasor Representation

\[\begin{aligned} v(t) & =\sqrt{2} V \cos \left(\omega t+\phi_{v}\right) \\ \Leftrightarrow \overrightarrow{V}& =V \angle \phi_{v} \\ i(t) & =\sqrt{2} I \cos \left(\omega t+\phi_{i}\right) \\ \Leftrightarrow \overrightarrow{I} & =I \angle \phi_{i} \end{aligned}\]

are in RMS and Note:

\[R i(t)+L \frac{d i(t)}{d t}+\frac{1}{C} \int i(t) \cdot d t=\sqrt{2} V \cos (\omega t)\]

use differential equation: To calculate

Time-domain, Phasor, & Impedance Triangle

\[\begin{aligned} Z & =R+j X_{L}+j X_{c} ~~ =|Z|<\phi \\ X_{L} & =\omega L, ~~ \quad X_{c}=\left(\frac{1}{-\omega C}\right) \\ |Z| & =\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}} & \phi=\tan ^{-1}\left[\frac{\left(\omega L-\frac{1}{\omega C}\right)}{R}\right] \end{aligned}\]

is complex but not a phasor, hence does not have time-domain expression Note:

Power and Power Factor

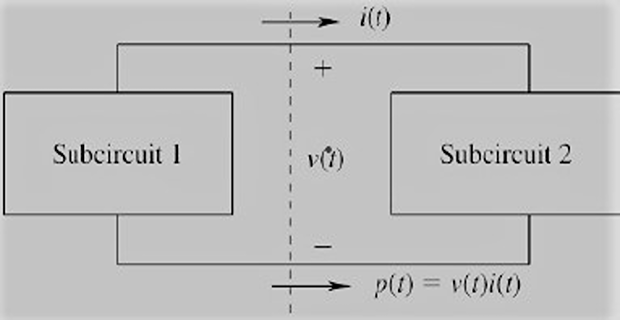
Instantaneous power \(p(t)=v(t)\cdot i(t)\) delivered by subcircuit-1 (Generator) is absorbed by subcircuit-2 (Load)
A negative value of \(p(t)\) reverses their role of delivering and absorbing power
Complex power (\(S\)), reactive power (\(Q\)), and power factor (pf) express how effectively active (average) power \(P\) transferred from one subcircuit to other

Instantaneous Power

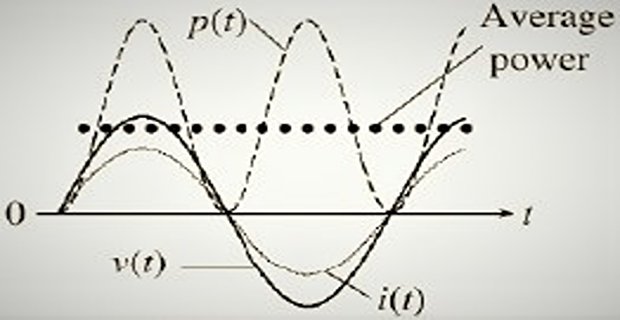
If \(v(t)\) and \(i(t)\) are in phase, \(p(t)\) pulsates at twice the steady-state \(f\)

\[\begin{aligned} p(t) & =\sqrt{2} V \cos \omega t \cdot \sqrt{2} I \cos \omega t \quad(i \text { in phase } \operatorname{with} v) \\ & = 2 V I \cos ^{2} \omega t=V I+V I \cos 2 \omega t \end{aligned}\]

are assumed to be zero without loss of generality and

In this case, for all times \(p(t) \geq 0\), and therefore power flows in only one direction from subcircuit 1 to 2
The average over one cycle of the second term of the RHS is zero, therefore average power is \(P= VI\)

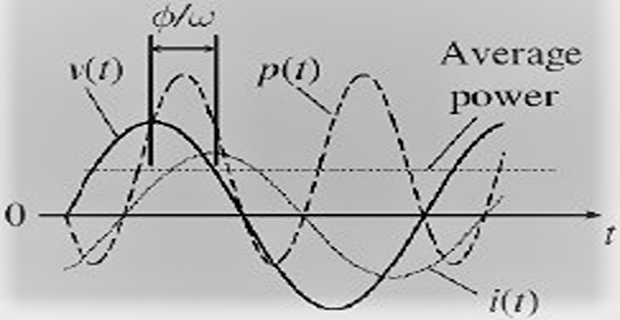
Considering \(i(t)\) lags behind \(v(t)\) by \(\phi (t)\)

\[\begin{aligned} p(t)& =\sqrt{2} V \cos \omega t \cdot \sqrt{2} I \cos (\omega t-\phi) \\ & =V I \cos \phi+V I \cos (2 \omega t-\phi) \end{aligned}\]
\(\phi/\omega\)\(p(t)\)
Negative \(p(t)\) means power flow in opposite direction
This back and forth flow of power indicates real power is not transferred from one subcircuit to other
Avg. power \(P=VI\cos\phi\) is less than the previous case

Powers: Active, Reactive, & Complex

Relationship between Power Quantities

\[\begin{aligned} S & =\overrightarrow{V}\overrightarrow{I}^{*} ~ *\rightarrow\text{conjugate}\\ & =V\angle\phi_{v}\cdot I\angle-\phi_{i}\\ & =VI\angle\left(\phi_{v}-\phi_{i}\right)\\ & =VI\angle\phi\\ & =P+jQ \end{aligned}\]

where,

\(I\cos \phi\) is in phase with \(V\), and results in \(P\)
\(I\sin \phi\) is at \(90^\circ\) to \(V\), and results in \(Q\)

Power Factor

\[\begin{aligned} P & =VI\cos\phi\\ \Rightarrow pf = \cos\phi & =\dfrac{P}{VI} =\dfrac{\text{Real Power}}{\text{Apparaent Power}}\\ & =\dfrac{kW}{kVA} =\dfrac{R}{Z} \end{aligned}\]

Units and Important Points

\[\begin{aligned} P & \rightarrow W(\text{Watts}); ~~ Q \rightarrow\text{VAR (Volt-Amperes Reactive)} \\ |S| & \rightarrow\text{VA (Volt-Amperes);} \\ \phi_{v},\phi_{i},\phi & \rightarrow\text{radians (+ve anticlockwise w.r.t real axis L to R)} \\ pf \rightarrow & \cos\phi = \text{ dimensionless, value between 0 to 1} \end{aligned}\]

Electrical usage cost is prop. to \(|S| = VI\)
Electrical insulation level and magnetic core size for a definite \(f\) depends on \(V\)
Conductor size depends on \(I\)
\(P\) represents (useful work \(+\) losses)
Desirable for \(Q = 0\) because it increases \(|S|\)
PF measure how effectively load draws \(P\)
Ideally \(P\) should be 1 (unity) i.e \(Q=0\)
Inductive load draws power at lagging pf (\(I\) lags \(V\))
Capacitive load draws power at leading pf (\(I\) leads \(V\))

\(P\) and \(Q\) in system

\[\begin{aligned} \text{Total Real Power} & =\sum_{k}P_{k}=\sum_{k}I_{k}^{2}R_{k}\\ \text{Total Reactive Power} & =\sum_{k}Q_{k}=\sum_{k}I_{k}^{2}X_{k} \\ +Q & \rightarrow \text{lagging load (Inductive)} \\ -Q & \rightarrow \text{leading load (Capacitive)} \end{aligned}\]

Importance of \(Q\)- Compensation