Solved Problems on 3-Phase Power
Demonstrative Video
Comparison Between Star and Delta Connections:
| Star Connection | Delta Connection | ||
|---|---|---|---|
| 1 | \(I_{L}=I_{ph}\) | \(I_{L}=\sqrt{3}I_{ph}\) | |
| 2 | \(V_{L}=\sqrt{3}V_{ph}\) | \(V_{L}=V_{ph}\) | |
| 3 | Total power = \(\sqrt{3}V_{L}I_{L}\cos\phi\) | = \(\sqrt{3}V_{L}I_{L}\cos\phi\) | |
| 4 | Per phase power = \(V_{ph}I_{ph}\cos\phi\) | = \(V_{ph}I_{ph}\cos\phi\) | |
| 5 | \(3\phi\) 3/4-wire systems are possible | \(3\phi\) 3-wire system is possible | |
| 6 | \(V_{L}\) lead the respective \(V_{ph}\) by \(30^{\circ}\) | \(I_{L}\) lag the respective \(I_{ph}\) by \(30^{\circ}\) |
Problem-1
A three-phase system with a line voltage of 400 V is supplying a delta-connected load of 1500 W at 0.8 pf lagging. Determine the phase and line currents and also the phase impedance.
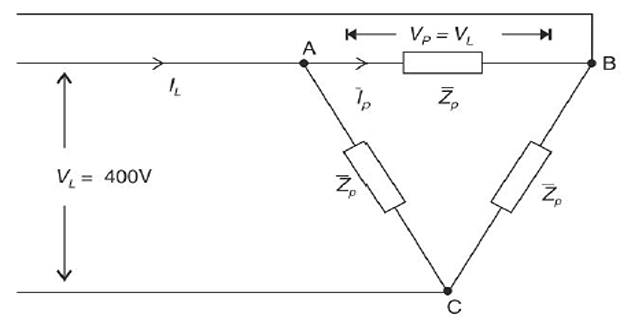
\[\begin{aligned} P(\text{per-phase}) & = \dfrac{1500}{3} = 500~\mathrm{W}\\ \text{For Delta-connection}~V_p & = V_L = 400~\mathrm{V} \\ P & = V_p \cdot I_p \cdot \cos\phi\\ \Rightarrow~500 & = 400 \cdot I_p \cdot 0.8~~ \Rightarrow~I_p = 1.56~\mathrm{A} \\ \text{For Delta-connection}~I_L & = \sqrt{3}I_p = 2.70~\mathrm{A} \\ Z_p & = \dfrac{V_p}{I_p} = \dfrac{400\angle 0^{\circ}}{2.70\angle-36.9^{\circ}} = 2.56\angle36.9^{\circ}~\Omega \end{aligned}\]
Problem-2
A 3-phase system supplies \(1200~ \mathrm{W}\) to a Star-connected load at 0.8 pf lagging. Determine the line and phase current and the phase impedance
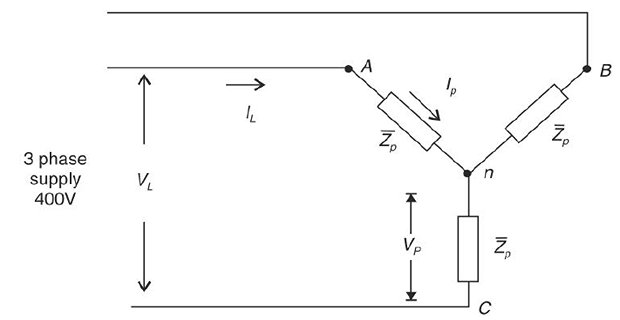
\[\begin{aligned} P(\text{per-phase})& = \dfrac{1200}{3} = 400~\mathrm{W} \\ \text{In Star-connection}~V_p & = \dfrac{V_L}{\sqrt{3}} = \dfrac{400}{\sqrt{3}} = 231~\mathrm{V} \\ P & = V_p \cdot I_p \cdot \cos\phi \qquad \left(\text{Note:}~ I_L = I_p \right)\\ \Rightarrow ~ 400 & = 231 \times I_p \times 0.8 ~\Rightarrow ~ I_p = 2.16~\mathrm{A}\\ \theta & = \cos^{-1}(0.8) = 36.9^{\circ}~(\text{lag})\\ Z_p & = \dfrac{V_p}{I_p} = \dfrac{231}{2.16\angle -36.9^{\circ}} = 106.9 \angle36.9^\circ ~\Omega \end{aligned}\]
Problem-3
A 400 V, three-phase, 50 Hz power supply is applied across the three terminals of a delta-connected three-phase load. The resistance and reactance of each phase is \(6~\Omega\) and \(8~\Omega\), respectively.
the line current and phase current
active, reactive, and apparent power of the circuit
The load is Delta-connected \[\begin{aligned} V_{\mathrm{Ph}}& =V_{\mathrm{L}}=400 \mathrm{~V} \\ Z_{\mathrm{Ph}} & =R+j \mathrm{X}=6+j 8=\sqrt{6^2+8^2} \angle \tan ^{-1} \frac{8}{6}=10 \angle 53^{\circ} \Omega \\ I_{\mathrm{Ph}} & =\frac{V_{\mathrm{Ph}}}{Z_{\mathrm{Ph}}}=\frac{400 \angle 0^{\circ}}{10 \angle 53^{\circ}}=40 \angle-53^{\circ} \mathrm{A} \\ \cos \phi & =\cos 53^{\circ}=0.6 \text { lagging } \\ I_{\mathrm{L}} & =\sqrt{3} I_{\mathrm{Ph}}=1.732 \times 40=69.28 \mathrm{~A} \\ \cos \phi & =\frac{R}{Z}=\frac{6}{10}=0.6 \text { lagging } \Rightarrow~ \sin \phi =0.8 \\ \end{aligned}\]
\[\begin{aligned} P &=\sqrt{3} V_{\mathrm{L}} I_{\mathrm{L}} \cos \phi=1.732 \times 400 \times 69.28 \times 0.6 \\ &=28798 \mathrm{~W}=28.798 \mathrm{~kW} \simeq 28.8 \mathrm{~kW} \\ Q &=\sqrt{3} V_{\mathrm{L}} I_{\mathrm{L}} \sin \phi=1.732 \times 400 \times 69.28 \times 0.8 \\ &=38397 \mathrm{VAR}=38.397 \mathrm{kVAR} \simeq 38.4 \mathrm{kVAR} \\ S &=3 V_{\mathrm{Ph}} I_{\mathrm{Ph}}=\sqrt{3} V_{\mathrm{L}} I_{\mathrm{L}} \\ &=1.732 \times 400 \times 69.28 \\ &=47997 \mathrm{VA}=47.997 \mathrm{kVA} \simeq 48 \mathrm{kVA} \end{aligned}\]
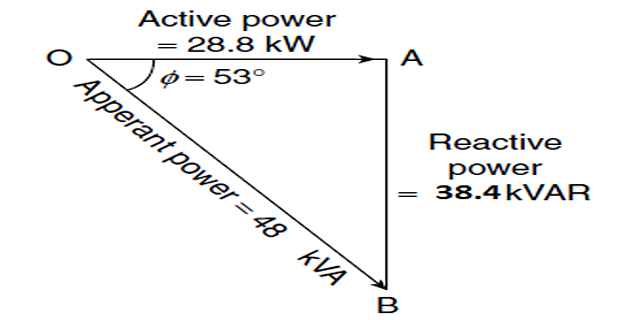 \[\begin{aligned}
S & = \sqrt{P^2+Q^2} \\
& = \sqrt{(28.8)^2+(38.4)^2} \\
&= 48 \mathrm{kVA}
\end{aligned}\]
\[\begin{aligned}
S & = \sqrt{P^2+Q^2} \\
& = \sqrt{(28.8)^2+(38.4)^2} \\
&= 48 \mathrm{kVA}
\end{aligned}\]
Problem-4
A \(3-\phi\), four-wire supply system has a line voltage of 400 V. Three non-inductive loads of 16 kW, 8 kW and 12 kW are connected between R, Y and B phases and the neutral, respectively. Calculate the neutral current?
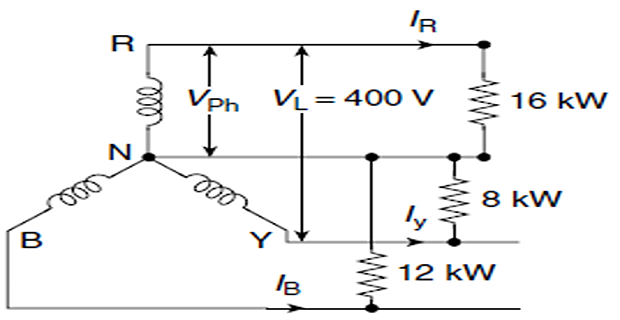
For star connection \(V_{\mathrm{Ph}}=\dfrac{V_{\mathrm{L}}}{\sqrt{3}}=\dfrac{400}{\sqrt{3}}=231 \mathrm{~V}\) \[ \begin{aligned} & V_{\mathrm{R}}=231 \angle 0^{\circ}, ~~V_{\mathrm{Y}}=231 \angle-120^{\circ}, \text { and }~~ V_{\mathrm{B}}=231 \angle-240^{\circ} \\ & I_{\mathrm{R}}=\frac{16 \times 1000}{V_{\mathrm{R}}}=\frac{16 \times 1000}{231 \angle 0}=69.3 \angle 0^{\circ} \\ & I_{\mathrm{Y}}=\frac{8 \times 1000}{V_{\mathrm{Y}}}=\frac{8 \times 1000}{231 \angle-240^{\circ}}=34.6 \angle 120^{\circ} \\ & I_{\mathrm{B}}=\frac{12 \times 1000}{V_{\mathrm{B}}}=\frac{12 \times 1000}{231 \angle-240^{\circ}}=52 \angle 240^{\circ} \\ & I_{\mathrm{N}}=I_{\mathrm{R}}+I_{\mathrm{Y}}+I_{\mathrm{B}} =26+j 75~\Rightarrow \left|I_{\mathrm{N}}\right| = 79.4~\mathrm{A} \end{aligned}\]
Problem-5
Each \(3-\phi\) has a load of resistance and reactance of \(6~\Omega\) each and connected in star. A 400 V, 50 Hz, \(3-\phi\) supply is connected across the load. Calculate phase voltage, phase current, power factor, power consumed per phase and the total power consumed by the load.
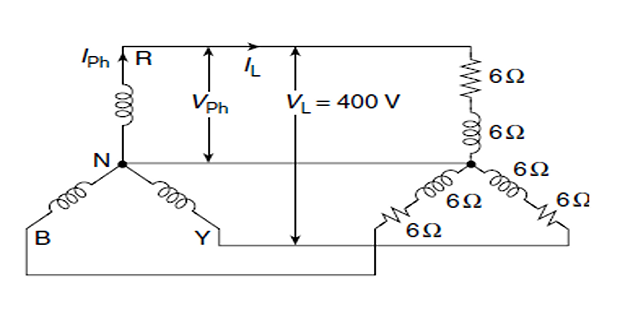
\[\begin{aligned} V_{\mathrm{Ph}} & =\frac{V_{\mathrm{L}}}{\sqrt{3}}=\frac{400}{\sqrt{3}}=231 \mathrm{~V} \\ Z_{\mathrm{Ph}} & =6+j 6 \mathrm{~W}=8.48 \angle 45^{\circ} \Omega \\ I_{\mathrm{Ph}} & =\frac{V_{\mathrm{Ph}}}{Z_{\mathrm{Ph}}}=\frac{231 \angle 0^{\circ}}{8.48 \angle 45^{\circ}}=27.2 \angle-45^{\circ} \mathrm{A} \\ I_{\mathrm{Ph}} & =I_{\mathrm{L}}=27.2 \mathrm{~A}\\ Pf &=\cos 45^{\circ}=0.7 ~\text{lagging} \end{aligned}\]
\[\begin{aligned} \text { Power absorbed by each load } & =V_{\mathrm{Ph}} I_{\mathrm{Ph}} \cos \phi \\ & =231 \times 27.2 \times 0.7 \\ & =4398 \mathrm{~W}\\ \text {Total power consumed}~ &=3 \times 4398=13194 \mathrm{~W} \end{aligned}\]
Problem-6
A balanced star-connected load of \((8+j 6) \Omega\) per phase is connected to a balanced three-phase, \(400 \mathrm{~V}\) supply. Find the line current, power factor, power and total volt-amperes.
\[\begin{aligned} \text{Phase voltage}~ V_{\mathrm{P}} & =\frac{\text { LineVoltage, } V_{\mathrm{L}}}{\sqrt{3}}=\frac{400}{\sqrt{3}}=231 \mathrm{~V} \\ \text{Impedance per phase}~Z_{\mathrm{P}} & =\sqrt{R^2+X_{\mathrm{L}}^2}=\sqrt{8^2+6^2}=10 \Omega \\ \text{Phase current}~I_{\mathrm{P}} & =\frac{V_{\mathrm{P}}}{Z_{\mathrm{P}}}=\frac{231}{10}=23.1 \mathrm{~A} \\ \text{ Line current}~I_{\mathrm{L}} & =I_{\mathrm{P}}=23.1 \mathrm{~A} \\ \text{Power factor}~\cos \phi & =\frac{R}{Z}=\frac{8}{10}=0.8 \text { (lagging) } \end{aligned}\]
\[\begin{aligned} \text{Total power}~P & =\sqrt{3} V_{\mathrm{L}} I_{\mathrm{L}} \cos \phi \\ & =\sqrt{3} \times 400 \times 23.1 \times 0.8 \\ & =12,800 \mathrm{~W} \\ \text{Total VA}~& =\sqrt{3} V_{\mathrm{L}} I_{\mathrm{L}} \\ & =\sqrt{3} \times 400 \times 23.1=16,000 \mathrm{VA} \end{aligned}\]
Problem-7
A three-phase star-connected load consumes a total of \(12 \mathrm{~kW}\) at a power factor of 0.8 lagging when connected to a \(400 \mathrm{~V}\), three-phase, \(50 \mathrm{~Hz}\) power supply. Calculate the resistance and inductance of load per phase.
\[\begin{aligned} \text{Total power consumed}&=12 \mathrm{~kW}\\ \text{Per phase power consumed}&=4 \mathrm{~kW}\\ V_{\mathrm{Ph}} I_{\mathrm{Ph}} \cos \phi & =4000 \mathrm{~W} \\ \Rightarrow~ I_{\mathrm{Ph}} & =\frac{4000}{V_{\mathrm{Ph}} \cos \phi} =\frac{4000}{(400 / \sqrt{3}) \times 0.8}=21.6 \mathrm{~A}\\ I_{\mathrm{Ph}}&=\frac{V_{\mathrm{Ph}}}{Z_{\mathrm{Ph}}} \Rightarrow~ Z_{\mathrm{Ph}}=\frac{V_{\mathrm{Ph}}}{I_{\mathrm{Ph}}}=\frac{231}{21.6}=10.7 \Omega\\ \text {Power factor } ~\cos \phi&=0.8, \qquad \Rightarrow \sin \phi=0.6 \end{aligned}\]
\[\begin{aligned} & R=Z_{\mathrm{Ph}} \cos \phi=10.7 \times 0.8=8.56 \Omega \\ & X=Z_{\mathrm{Ph}} \sin \phi=10.7 \times 0.6=6.42 \Omega \\ & X=6.42 \\ & 2 \pi f L=6.42 \\ & L=\frac{6.42}{2 \times 3.14 \times 50}=20.4 \times 10^{-3} \mathrm{H} \\ &=20.4 \mathrm{mH} \end{aligned}\]