Solved Problems on Super Mesh Analysis
Demonstrative Video
Problem-1
Find the current flowing through \(R_3\) ?
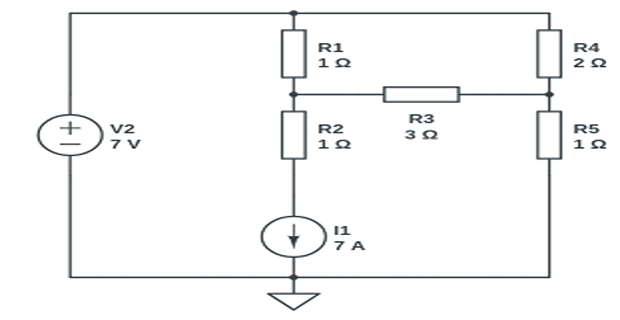
Solution-1
Applying KVL in supermesh-1 and 3 and mesh analysis in loop-2 \[\begin{aligned} -7+(i1-i2)+3(i3-i2)+i3 & = 0\\ (i2-i1)+2i2+3(i2-i3) & = 0\\ i1-i3 & = 7 \end{aligned}\]
Solutions: \(i_1= 9~\mathrm{A} \quad i_2 = 2.5~\mathrm{A} \quad i_3 = 2~\mathrm{A}\)
Problem-2
Find the current flowing through \(V_2\) ?
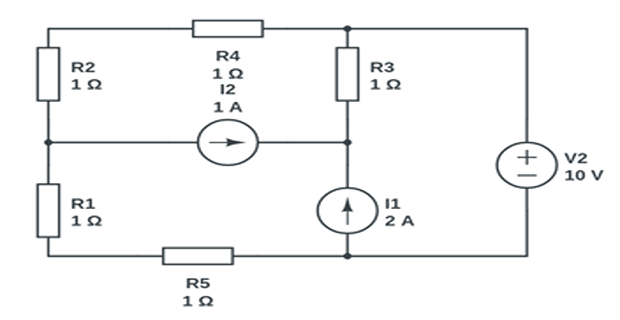
Solution-2
KVL in supermesh \[\begin{aligned} -10 -2I_1 - 2I_2 & =0\\ I_3-I_2 &= 2\\ I_2-I_1 &= 1 \end{aligned}\]
solutions: \[I_1=-3 ~\mathrm{A} \quad I_2 = -2 ~\mathrm{A} \quad I_3= 0~\mathrm{A}\]
Problem-3
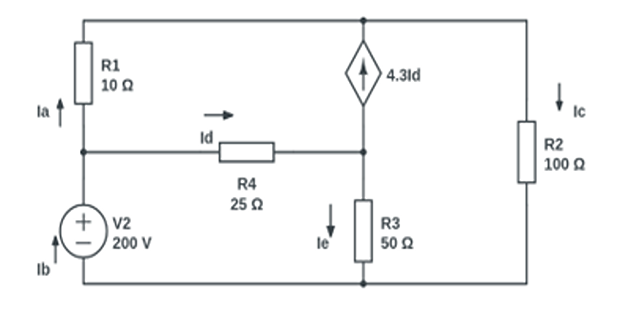
Determine \(I_a\), \(I_b\), \(I_c\), \(I_d\), \(I_e\) ?
Solution-3
Equations \[\begin{aligned} -10I_1-100I_2-50(I_2-I_3)-25(I_1-I_3)& = 0 \\ 200-25(I_3-I_1)-50(I_3-I_2)& = 0 \\ (I_2-I_1)&=4.3(I_3-I_1) \end{aligned}\]
Solutions:
\[\begin{aligned} I_1&=7.403~\mathrm{A}\\ I_2&= 1.26~\mathrm{A}\\ I_3&= 5.97~\mathrm{A} \end{aligned}\] \[\begin{aligned} \mathrm{I_a}&=7.40 \mathrm{~A} \quad \mathrm{I_b}=5.97 \mathrm{~A}\\ \mathrm{I_c}&=1.26 \mathrm{~A} \quad \mathrm{I_d}=-1.43 \mathrm{~A}\\ \mathrm{I_e}&=4.71 \mathrm{~A} \end{aligned}\]
Problem-4
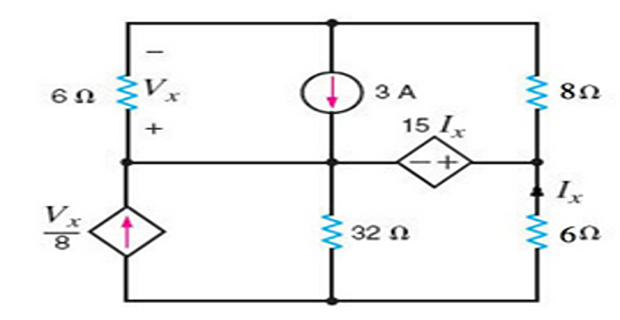
Find \(V_x\) and \(I_x\)
Solution-4
Equations: \[\begin{aligned} -6I_1-8I_2-15I_x&=0 \\ I_1-I_2& = 3 \\ -32(I_3-I_4)+15I_x-6I_3& = 0 \\ I_x &= -I_3 \\ I_4 &= V_x/8 \\ V_x & = 6I_1 \end{aligned}\]
Solutions:
\[\begin{aligned} I_1 & = 3.33~\mathrm{A}\\ I_2 & = 0.3298~\mathrm{A}\\ I_3 & = 1.508~\mathrm{A}\\ I_4 & = 2.497 ~\mathrm{A}\\ \end{aligned}\] \[\begin{aligned} I_x & = -1.508~\mathrm{A}\\ V_x & = 19.98~\mathrm{V} \end{aligned}\]
Problem-5
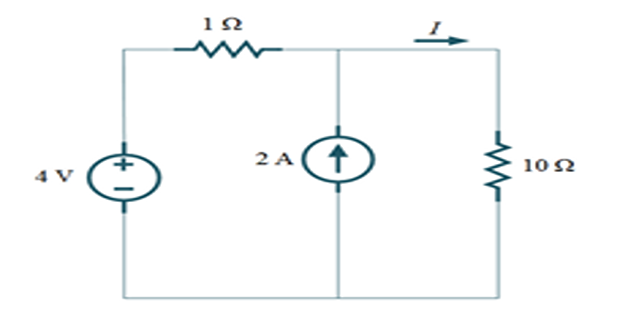
Find currents in both resistors?
Solution-5
Equations: \[\begin{aligned} 4-I_1-10I_2 & = 0\\ I_2-I_1 & = 2 \end{aligned}\]
Solutions: \[I_1 = -1.455 ~\mathrm{A} \quad I_2 = 0.5455 ~\mathrm{A}\]
Problem-6
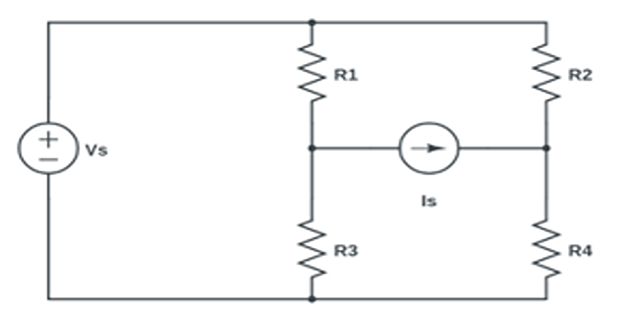\[V_{S}=10
V,~ I_{S}=4 A,~ R_{1}=2 \Omega,~ R_{2}=6 \Omega, ~ R_{3}=1 \Omega,~
R_{4}=2 \Omega\]
Find power of sources?
Solution-6
Equations: \[\begin{aligned} V_s - R_1(I_1-I_2) - R_3(I_1-I_3) & = 0 \\ -R_1(I_2-I_1)-I_2R_2-I_3R_4-(I_3-I_1)R_3&=0 \\ I_3-I_2&=I_s\\ \end{aligned}\]
Solutions: \[\begin{aligned} I_1 &= 4.92~\mathrm{A} \\ I_2 & = 0.25~\mathrm{A}\\ I_3& = 4.25~\mathrm{A} \end{aligned}\]
\[\begin{aligned} &P_{V_{S}}=-V_{S} \times I_{1}=-49.2 \mathrm{~W} \\ &V_{I_{S}}=2 \times(0.25-4.92)+6 \times 0.25\\ &= -7.84 \mathrm{~V} \\ &P_{I_{S}}=V_{I_{S}} \times I_{S}\\ &=-7.84 \times 4=-31.36 \mathrm{~W} \end{aligned}\]
Problem-7
Find the currents \(i_1\) to \(i_4\) using Mesh analysis?
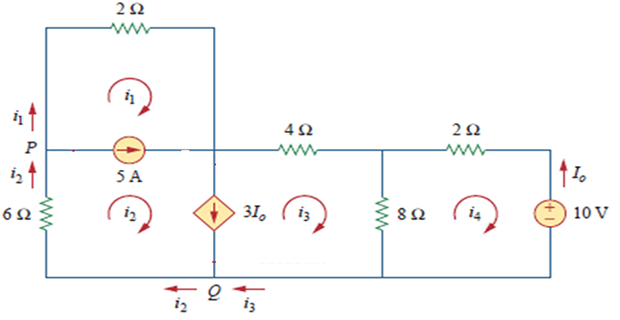
Solution-7
Meshes 1 and 2: Supermesh with independent common current source
Meshes 2 and 3: Supermesh with dependent common current source
The two supermesh intersect to form a larger supermesh
Apply KVL in larger supermesh \[\begin{aligned} 2i_1+4i_3+8(i_3-i_4)+6i_2 & = 0 \\ i_1+3i_2+6i_3-4i_4 & = 0 \end{aligned}\]
KCL at Node-P \[i_2 = i_1+5\]
KCL to node-Q \[\begin{aligned} i_2&=i_3+3I_0 \Rightarrow i_2=i_3-3i_4~(I_0=-i_4) \end{aligned}\]
KVL in mesh-4 \[\begin{aligned} 2i_4+8(i_4-i_3)+10&=0\\ \Rightarrow 5i_4-4i_3&=-5 \end{aligned}\]
Solving the following equations \[\begin{aligned} i_1+3i_2+6i_3-4i_4&=0\\ i_2&=i_1+5\\ i_2&=i_3-3i_4\\ 5i_4-4i_3&=-5 \end{aligned}\]
Solutions: \[i_{1}=-7.5 \mathrm{~A}, \quad i_{2}=-2.5 \mathrm{~A}, \quad i_{3}=3.93 \mathrm{~A}, \quad i_{4}=2.143 \mathrm{~A}\]