Solved Problems on Single-Phase AC Power
Demonstrative Video
Problem-1
Determine the power factor of the circuit as seen by the source.
Calculate the average power delivered by the source.
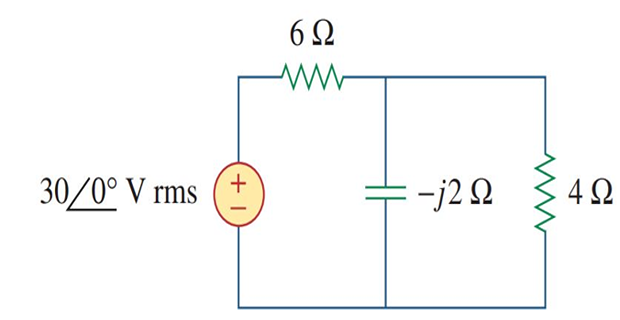
The total impedance is \[\mathbf{Z}=6+4 \|(-j 2)=6+\frac{-j 2 \times 4}{4-j 2}=6.8-j 1.6=7 \angle-13.24^{\circ} \Omega\] The power factor is \[\mathrm{pf}=\cos (-13.24)=0.9734 \quad \text { (leading) }\] since the impedance is capacitive. The rms value of the current is \[\mathbf{I}_{\mathrm{rms}}=\frac{\mathbf{V}_{\mathrm{rms}}}{\mathbf{Z}}=\frac{30 \angle 0^{\circ}}{7 \angle-13.24^{\circ}}=4.286 \angle 13.24^{\circ} \mathrm{A}\]
The average power supplied by the source is \[P=V_{\mathrm{rms}} \cdot I_{\mathrm{rms}} \cdot \mathrm{pf}=(30)(4.286) 0.9734=125 \mathrm{~W}\] or \[P=I_{\mathrm{rms}}^2 R=(4.286)^2(6.8)=125 \mathrm{~W}\] where \(R\) is the resistive part of \(\mathbf{Z}\).
Problem-2
The voltage across a load is \(v(t)=60 \cos \left(\omega t-10^{\circ}\right) \mathrm{V}\) and the current through the element in the direction of the voltage drop is \(i(t)=1.5 \cos \left(\omega t+50^{\circ}\right)\) A. Find:
the complex and apparent powers,
the real and reactive powers,
the power factor and the load impedance.
\(v(t)=60 \cos \left(\omega t-10^{\circ}\right) \mathrm{V}~~\qquad~~i(t)=1.5 \cos \left(\omega t+50^{\circ}\right)\) \[\begin{aligned} \text{RMS Quantities}~ \mathbf{V}_{\mathrm{rms}} & =\frac{60}{\sqrt{2}} \angle-10^{\circ}, \quad \mathbf{I}_{\mathrm{rms}}=\frac{1.5}{\sqrt{2}} \angle+50^{\circ} \\ \text{Complex power}~\mathbf{S} & =\mathbf{V}_{\text {rms }} \mathbf{I}_{\text {rms }}^*\\ &=\left(\frac{60}{\sqrt{2}} \angle-10^{\circ}\right)\left(\frac{1.5}{\sqrt{2}} \angle-50^{\circ}\right)=45 \angle-60^{\circ} \mathrm{VA} \\ \text{Apparent power}~ S & =|\mathbf{S}|=45 \mathrm{VA} \\ \text{Rectangular form}~\mathbf{S} & =45 \angle-60^{\circ}=45\left[\cos \left(-60^{\circ}\right)+j \sin \left(-60^{\circ}\right)\right]\\ &=22.5-j 38.97 \\ &= P+jQ\\ \Rightarrow~P & = 22.5~\mathrm{W} \quad \Rightarrow~Q = -38.97~\mathrm{VAR}~(\text{-ve capacitive}) \\ \text{Power factor}~pf & = \cos(-60^{\circ}) = 0.5~\left(\text{leading}\right) \\ \text{Load impedance}~\mathbf{Z} & = \dfrac{\mathbf{V}}{\mathbf{I}} = \dfrac{60\angle{-10^{\circ}}}{1.5\angle{+50^{\circ}}} = 40\angle{-60^{\circ}}~\Omega \end{aligned}\]
Problem-3
A load \(\mathbf{Z}\) draws \(12~ \mathrm{kVA}\) at a power factor of
0.856 lagging from a \(120~V\) rms
sinusoidal source.
Calculate:
the average and reactive powers delivered to the load
the peak current
the load impedance.
\[\begin{aligned} pf & = \cos\theta = 0.856~(\text{Given}) \Rightarrow \theta = 31.13^{\circ}\\ S & = 12000~\text{VA}~(\text{Given}) \\ \Rightarrow P & = S\cos\theta = 12000\times 0.856 = 10.272~\mathrm{kW}\\ \Rightarrow Q & = S\sin\theta = 12000\times 0.517 = 6.204~\mathrm{kVA}\\ \mathbf{S} & = P+jQ = 10.272 +j 6.204\\ \mathbf{I^{\ast}_{rms}} &= \dfrac{\mathbf{S}}{\mathbf{V_{rms}}} = \dfrac{10.272 +j 6.204}{120\angle 0^{\circ}} = 100\angle 31.13^{\circ}~\mathrm{A} \\ I_m & = \sqrt{2} \mathbf{I_{rms}} = \sqrt{2}\times 100 =141.4~\mathrm{A} \\ \mathbf{Z} & = \dfrac{\mathbf{V_{rms}}}{\mathbf{I_{rms}}} = \dfrac{120\angle 0^{\circ}}{100\angle -31.13^{\circ}} = 1.2\angle 31.13^{\circ}~\Omega \end{aligned}\]
Problem-4
Conservation of AC Power:
A load operates at 20 kW, 0.8 pf lagging. The load voltage is \(220\angle 0^{\circ}\) V rms at 60 Hz. The impedance of the line is \(0.09+j0.3~\Omega\). Determine the voltage and power factor at the input to the line.
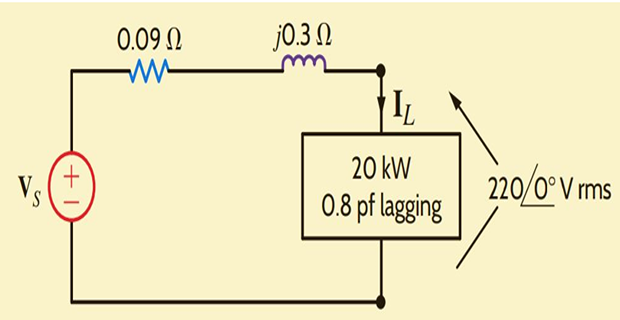
\[\begin{aligned} S & = \dfrac{P}{\cos\theta} = \dfrac{P}{pf} = \dfrac{20,000}{0.8} = 25,000~\mathrm{VA} \\ \mathbf{S_L} & = 25,000\angle 36.87^{\circ} = 20,000 + j15,000~\mathrm{VA} \\ \mathbf{I_L} & = \left[\dfrac{\mathbf{S_L}}{\mathbf{V_L}}\right]^{\ast}= \left[\dfrac{25,000\angle 36.87^{\circ} }{220\angle 0^{\circ} }\right]^{\ast}\\ & = 113.64\angle -36.87^{\circ}~\mathrm{Arms} \end{aligned}\]
\[\begin{aligned} \mathbf{S}_{\text {line }} & =I_L^2 \mathbf{Z}_{\text {line }} \\ & =(113.64)^2(0.09+j 0.3) \\ & =1162.26+j 3874.21 \mathrm{VA} \\ \mathbf{S}_S & =\mathbf{S}_L+\mathbf{S}_{\text {line }} \\ & =21,162.26+j 18,874.21 \\ & =28,356.25 \angle 41.73^{\circ} \mathrm{VA} \\ V_S & =\frac{\left|S_S\right|}{I_L}=\frac{28,356.25}{113.64} \\ & =249.53 \mathrm{~V} \mathrm{rms} \\ pf~\cos \left(41.73^{\circ}\right) & =0.75 \text { lagging } \end{aligned}\] Note: We could have alternatively solved the problem using KVL
Alternative method using KVL: \[\begin{aligned} \mathbf{I}_L & =113.64 \angle-36.87^{\circ} \mathrm{A} \mathrm{rms} \\ \mathbf{V}_{\text {line }} & =\left(113.64 \angle-36.87^{\circ}\right)(0.09+j 0.3) \\ & =35.59 \angle 36.43^{\circ} \mathrm{V} \mathrm{rms} \\ \mathbf{V}_S & =220 \angle 0^{\circ}+35.59 \angle 36.43^{\circ} \\ & =249.53 \angle 4.86^{\circ} \mathrm{V} \mathrm{rms} \\ \theta_v-\theta_i & =4.86^{\circ}-\left(-36.87^{\circ}\right)=41.73^{\circ} \\ \mathrm{pf} & =\cos \left(41.73^{\circ}\right)=0.75 \text { lagging } \end{aligned}\]
Problem-5
A series-connected load draws a current \(i(t)=4 \cos \left(100 \pi t+10^{\circ}\right) \mathrm{A}\) when the applied voltage is \(v(t)=120 \cos \left(100 \pi t-20^{\circ}\right) \mathrm{V}\).
Find the apparent power and the power factor of the load.
Determine the element values that form the series-connected load.
Given data:
\(i(t)=4 \cos \left(100 \pi
t+10^{\circ}\right) \mathrm{A}~~ \qquad v(t)=120 \cos \left(100 \pi
t-20^{\circ}\right) \mathrm{V}\) \[\begin{aligned}
& S=V_{\mathrm{rms}} \cdot
I_{\mathrm{rms}}=\frac{120}{\sqrt{2}} \frac{4}{\sqrt{2}}=240 \mathrm{VA}
\\
& \mathrm{pf}=\cos \left(\theta_v-\theta_i\right)=\cos
\left(-20^{\circ}-10^{\circ}\right)=0.866 \quad \text { (leading) } \\
\text{Alternatively} & \\
& \mathbf{Z}=\frac{\mathbf{V}}{\mathbf{I}}=\frac{120
\angle-20^{\circ}}{4 \angle 10^{\circ}}=30 \angle-30^{\circ}\\
&=25.98-j 15 ~\Omega =R-jX_c \Rightarrow~R = 25.98~\Omega \\
& \mathrm{pf}=\cos \left(-30^{\circ}\right)=0.866 \quad
\text { (leading) } \\
& X_C=-15=-\frac{1}{\omega C} \\
\Rightarrow~& C=\frac{1}{15 \omega}=\frac{1}{15 \times 100
\pi}=212.2 \mu \mathrm{F}
\end{aligned}\]
Problem-6
Find the total complex power and the input power factor?
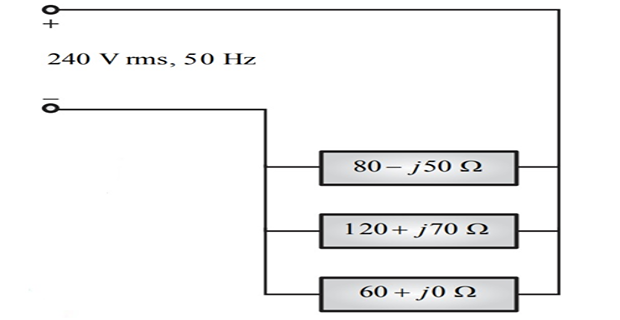
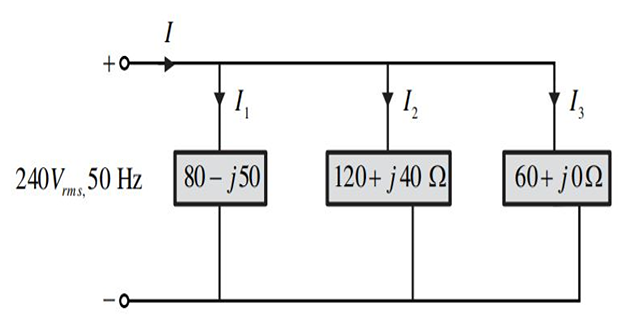\[\begin{aligned}
I &=I_1+I_2+I_3 \\
& =\frac{240}{80-j 50}+\frac{240}{120+j 70}+\frac{240}{60+j
0} \\
& =(7.644+j 0.4776) \mathrm{A} \\
I^* &=(7.644-j 0.4776) \mathrm{A} \\
S & =V I^* \\
& =240\left[7.644-j 0.4776\right] \\
& =\left(1.8345-j 0.1146\right) ~\mathrm{kVA}
\end{aligned}\]
Problem-7
Maximum Power Transfer Theorem:
Find the value of \(R_L\) that will absorb the maximum average power? Calculate that power.
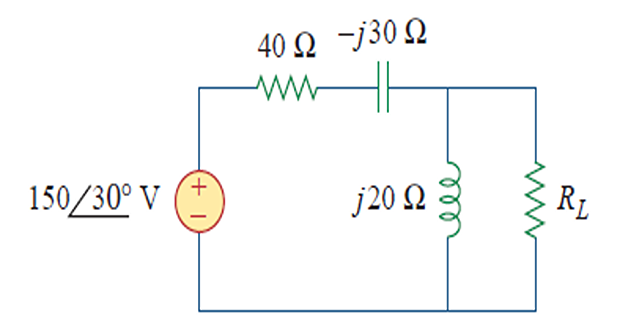
\[\begin{aligned} \mathbf{Z}_{\mathrm{Th}}&=(40-j 30) \| j 20=\frac{j 20(40-j 30)}{j 20+40-j 30}=9.412+j 22.35 \Omega \\ \mathbf{V}_{\mathrm{Th}}&=\frac{j 20}{j 20+40-j 30}\left(150 \angle 30^{\circ}\right)=72.76 \angle 134^{\circ} \mathrm{V} \\ R_L&=\left|\mathbf{Z}_{\mathrm{Th}}\right|=\sqrt{9.412^2+22.35^2}=24.25 \Omega \\ \mathbf{I}&=\frac{\mathbf{V}_{\mathrm{Th}}}{\mathbf{Z}_{\mathrm{Th}}+R_L}=\frac{72.76 \angle 134^{\circ}}{33.66+j 22.35}=1.8 \angle 100.42^{\circ} \mathrm{A} \\ P_{\max }&=\frac{1}{2}|\mathbf{I}|^2 R_L=\frac{1}{2}(1.8)^2(24.25)=39.29 \mathrm{~W} \end{aligned}\]
Problem-8
Given : \(Z_1 = 60 \angle -30^{\circ}~\Omega\) and \(Z_2 = 40 \angle 45^{\circ}~\Omega\). Calculate the total: (a) apparent power, (b) real power, (c) reactive power, and (d) pf, supplied by the source and seen by the source
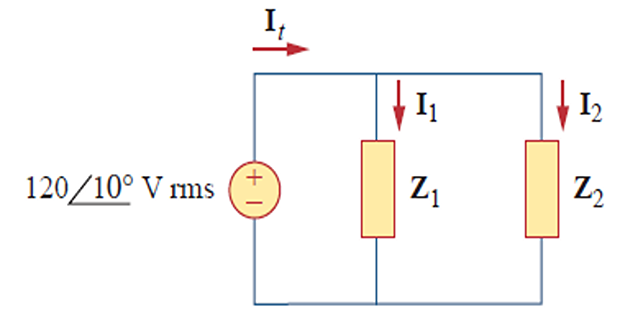
\[\begin{aligned} \mathbf{I}_1 & =\frac{\mathbf{V}}{\mathbf{Z}_1}=\frac{120 \angle 10^{\circ}}{60 \angle-30^{\circ}}=2 \angle 40^{\circ} \mathrm{A} \mathrm{rms} \\ \mathbf{I}_2 & =\frac{\mathbf{V}}{\mathbf{Z}_2}=\frac{120 \angle 10^{\circ}}{40 \angle 45^{\circ}}=3 \angle-35^{\circ} \mathrm{A} \mathrm{rms} \\ \mathbf{S}_1 & =\frac{V_{\mathrm{rms}}^2}{\mathbf{Z}_1^*}=\frac{(120)^2}{60 \angle 30^{\circ}}=240 \angle -30^{\circ}=207.85-j 120 \mathrm{VA} \\ \mathbf{S}_2 & =\frac{V_{\mathrm{rms}}^2}{\mathbf{Z}_2^*}=\frac{(120)^2}{40 \angle-45^{\circ}}=360 \angle 45^{\circ}=254.6+j 254.6 \mathrm{VA} \end{aligned}\]
\[\begin{aligned} \mathbf{S}_t & =\mathbf{S}_1+\mathbf{S}_2=462.4+j 134.6 \mathrm{VA} \\ \left|\mathbf{S}_t\right| & =\sqrt{462.4^2+134.6^2}=481.6 \mathrm{VA} \\ P_t & =\operatorname{Re}\left(\mathbf{S}_t\right)=462.4 \mathrm{~W} \text { or } P_t=P_1+P_2 . \\ Q_t & =\operatorname{Im}\left(\mathbf{S}_t\right)=134.6 \mathrm{VAR} \text { or } Q_t=Q_1+Q_2 \\ \mathrm{pf} & =P_t /\left|\mathbf{S}_t\right|=462.4 / 481.6=0.96(\text { lagging }) \end{aligned}\] Verify using complex power of the source: \[\begin{aligned} \mathbf{I}_t=\mathbf{I}_1+\mathbf{I}_2 & =(1.532+j 1.286)+(2.457-j 1.721) \\ & =4-j 0.435=4.024 \angle-6.21^{\circ} \mathrm{Arms} \\ \mathbf{S}_s=\mathbf{V} \mathbf{I}_t^* & =\left(120 \angle 10^{\circ}\right)\left(4.024 \angle 6.21^{\circ}\right) \\ & =482.88 \angle 16.21^{\circ}=463+j 135 \mathrm{VA} \end{aligned}\]