Solved Problems on 3-Phase Power Measurement by 2-Wattmeter
Demonstrative Video
Problem-1
Find the total power absorbed?
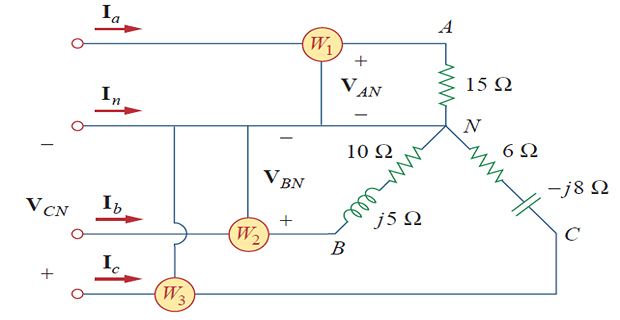
Given : \[\begin{aligned} \mathbf{V}_{AN} & = 100\angle 0^{\circ}, \quad \mathbf{V}_{BN} = 100 \angle 120^{\circ}, \quad \mathbf{V}_{CN} = 100 \angle -120^{\circ}~\mathrm{V} \\ \mathbf{I}_{a} & = 6.67 \angle 0^{\circ}, \quad \mathbf{I}_{b} = 8.94\angle 93.44^{\circ}, \quad \mathbf{I}_{c} = 10 \angle -66.87^{\circ}~\mathrm{A} \end{aligned}\]
\[\begin{aligned} & P_1=\operatorname{Re}\left(\mathbf{V}_{A N} \mathbf{I}_a^*\right)=V_{A N} I_a \cos \left(\theta_{\mathbf{V}_{A N}}-\theta_{\mathbf{I}_a}\right) \\ &=100 \times 6.67 \times \cos \left(0^{\circ}-0^{\circ}\right)=667 \mathrm{~W} \\ & P_2=\operatorname{Re}\left(\mathbf{V}_{B N} \mathbf{I}_b^*\right)=V_{B N} I_b \cos \left(\theta_{\mathbf{V}_{B N}}-\theta_{\mathbf{I}_b}\right) \\ &=100 \times 8.94 \times \cos \left(120^{\circ}-93.44^{\circ}\right)=800 \mathrm{~W} \\ & P_3=\operatorname{Re}\left(\mathbf{V}_{C N} \mathbf{I}_c^*\right)=V_{C N} I_c \cos \left(\theta_{\mathbf{V}_{C N}}-\theta_{\mathbf{I}_c}\right) \\ &=100 \times 10 \times \cos \left(-120^{\circ}+66.87^{\circ}\right)=600 \mathrm{~W} \\ & P_T= P_1+P_2+P_3=667+800+600=2067 \mathrm{~W} \end{aligned}\] Validation: \[\begin{aligned} & P_T=\left|I_a\right|^2(15)+\left|I_b\right|^2(10)+\left|I_c\right|^2(6) \\ &=6.67^2(15)+8.94^2(10)+10^2(6) \\ &=667+800+600=2067 \mathrm{~W} \end{aligned}\]
Problem-2
The two-wattmeter method produces readings \(P_1 = 1560~\mathrm{W}\) and \(P_2 = 2100~\mathrm{W}\) and when connected to a delta-connected load. If the line voltage is 220 V, calculate:
the per-phase average power,
the per-phase reactive power,
the power factor, and
the phase impedance.
\[\begin{aligned} P_T & =P_1+P_2=1560+2100=3660 \mathrm{~W} \\ P_p & =\frac{1}{3} P_T=1220 \mathrm{~W} \\ Q_T & =\sqrt{3}\left(P_2-P_1\right)=\sqrt{3} \cdot(2100-1560)=935.3 \mathrm{VAR} \\ Q_p & =\frac{1}{3} Q_T=311.77 \mathrm{~VAR} \\ \theta & =\tan ^{-1} \frac{Q_T}{P_T}=\tan ^{-1} \frac{935.3}{3660}=14.33^{\circ} \\ \cos \theta & =0.9689~(\text { lagging }) \\ P_p & =V_p I_p \cos \theta \Rightarrow I_p = \dfrac{1220}{220 \times 0.9689} = 5.723~\mathrm{A} \quad (V_p = V_L = 220)\\ Z_p & =\frac{V_p}{I_p}=\frac{220}{5.723}=38.44 \Omega \\ \mathbf{Z}_p & =38.44 \angle 14.33^{\circ} \Omega \end{aligned}\]
Problem-3
The three-phase balanced load has impedance per phase of \(\mathbf{Z}_Y=8+j 6 \Omega\). If the load is connected to \(208-\mathrm{V}\) lines, predict the readings of the wattmeters \(W_1\) and \(W_2\). Find \(P_T\) and \(Q_T\).
The impedance per phase is \[\mathbf{Z}_Y=8+j 6=10 \angle 36.87^{\circ} \Omega\]
so that the pf angle is \(36.87^{\circ}\).
Since the line voltage \(V_L=208 \mathrm{~V}\), the line current is \[I_L=\frac{V_p}{\left|\mathbf{Z}_Y\right|}=\frac{208 / \sqrt{3}}{10}=12 \mathrm{~A}\]
Then watt meter readings \[\begin{aligned} P_1 & =V_L I_L \cos \left(\theta+30^{\circ}\right)=208 \times 12 \times \cos \left(36.87^{\circ}+30^{\circ}\right) \\ & =980.48 \mathrm{~W} \\ P_2 & =V_L I_L \cos \left(\theta-30^{\circ}\right)=208 \times 12 \times \cos \left(36.87^{\circ}-30^{\circ}\right) \\ & =2478.1 \mathrm{~W} \end{aligned}\]
Wattmeter 1 reads \(980.48 \mathrm{~W}\), while wattmeter 2 reads \(2478.1 \mathrm{~W}\).
\(P_2>P_1 \Rightarrow\) inductive load.
This is evident from the load \(\mathbf{Z}_Y\) itself.
Finally \[\begin{aligned} P_T & =P_1+P_2=3.459 \mathrm{~kW} \\ Q_T & =\sqrt{3}\left(P_2-P_1\right)=\sqrt{3}(1497.6) \mathrm{VAR}=2.594 \mathrm{~kVAR} \end{aligned}\]