Solved Problems on Nodal Analysis
Demonstrative Video
Problem-1
If \(R=0\) and the current \(i_R = 10\) A. Find the value of \(E\) ?
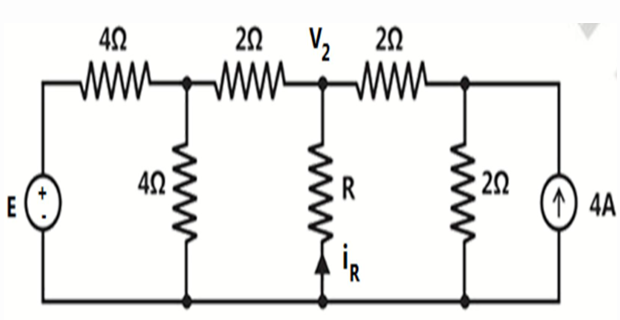
Solution-1
\(R=0\) means short circuit and the top node voltage is same as ref. node (0V)
Applying nodal analysis at node-1 \[\begin{aligned} \dfrac{V_1-E}{4}+ \dfrac{V_1}{4}+\dfrac{V_1}{2} & =0 \Rightarrow E = 4V_1 \end{aligned}\]
At Node-2 (last node) \[\begin{aligned} \dfrac{V_2-0}{2}+\dfrac{V_2}{2} & = 4 \Rightarrow V_2 = 4\mathrm{V} \end{aligned}\]
The KCL for \(I_R\) is \[\begin{aligned} I_R & = \dfrac{0-V_1}{2}+\dfrac{0-V_2}{2} \end{aligned}\]
Substituting \(I_R=10\) A and \(V_2 = 4\mathrm{V}\), we get \[V_1 = -24~\mathrm{V}\]
Finally, \(E = 4V_1 = -96~\mathrm{V}\)
Problem-2
Using Nodal analysis, find the current in the resistors?
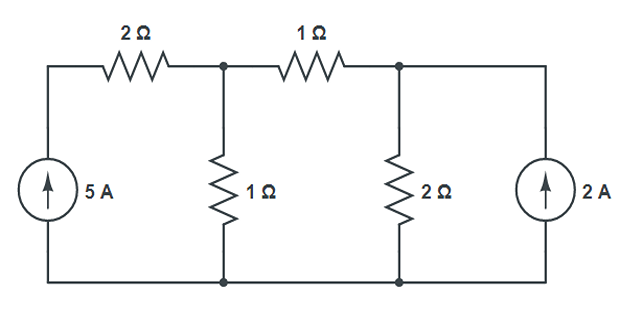
Solution-2
At Node-1 \[-5+\dfrac{V_1}{1}+\dfrac{V_1-V_2}{1}=0\]
At Node-2 \[-2 + \dfrac{V_2}{2}+\dfrac{V_2-V_1}{1} =0\]
Solving \(V_1= 0.25\) V and \(V_2 = -4.5\) V
Current in the resistors can be found using ohm’s law \(I=V/R\)
Problem-3
Find the values of \(V1\) and \(V2\) ?
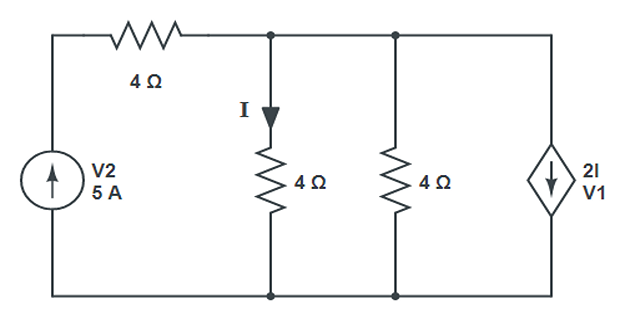
Solution-3
Applying KCl at Node \[-5+\dfrac{V}{4}+\dfrac{V}{4}+2I=0\]
Also \[I = \dfrac{V}{4}\]
Solution \[V_1 = 5~\mathrm{V} \quad V_2 = 25~\mathrm{V}\]
Problem-4
Find the Node voltages?
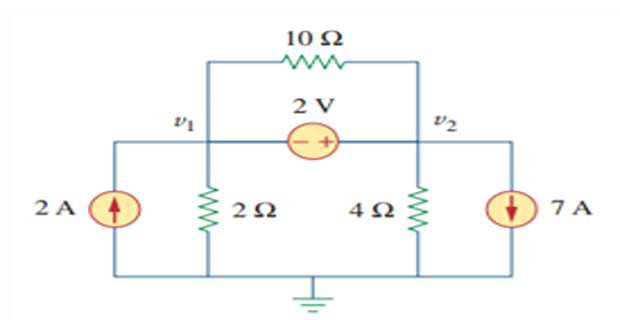
Solution-4
Combining super-nodes \(v_1\) - \(v_2\) \[\begin{aligned} -2+\dfrac{v_1}{2}+\dfrac{v_2}{4}+7&=0 \end{aligned}\]
Super-node voltage constraint equation: \[v_2-v_1 = 2\]
On solving, we get \[v_1 = -7.333~\mathrm{V} \quad v_2 = -5.333~\mathrm{V}\]
Note: 10\(\Omega\) resistor do not make any difference because it is connected across super-node.
Problem-5
Find the power of the dependent current source?
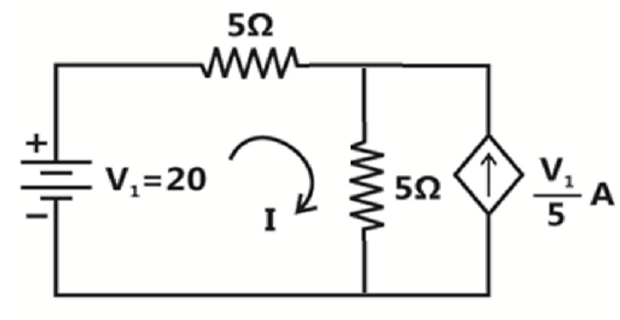
Solution-5
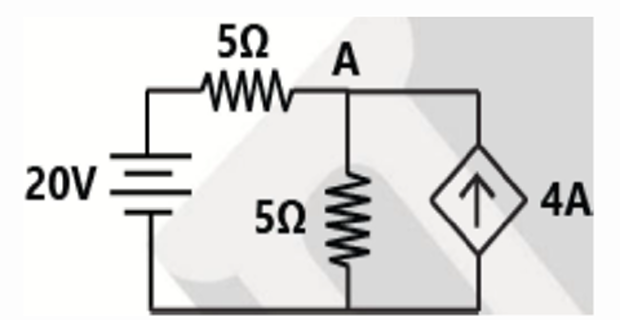
Apply KCL at node-A \[\begin{aligned} \dfrac{V_A-20}{5}+\dfrac{V_A}{5} & = 4 \\ \Rightarrow V_A & = 20~\mathrm{V} \end{aligned}\]
Power delivered by the dependent source \[=20\times 4 = 80~\mathrm{W}\]
Problem-6
Find the current through the 5\(\Omega\) resistor?
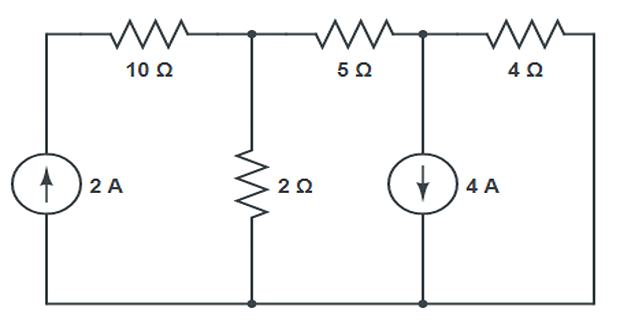
Solution-6
Apply KCL at node-1 \[\begin{aligned} -2+\dfrac{V_1}{2}+\dfrac{V_1-V_2}{5}&=0 \end{aligned}\]
Apply KCL at node-2 \[\begin{aligned} -\dfrac{V_1-V_2}{5}+4+\dfrac{V_2}{4}&=0 \end{aligned}\]
On solving, we get \[V_1 = 0.4~\mathrm{V} \quad V_2 = -8.7~\mathrm{V}\]
Problem-7
Find \(V1\) ?
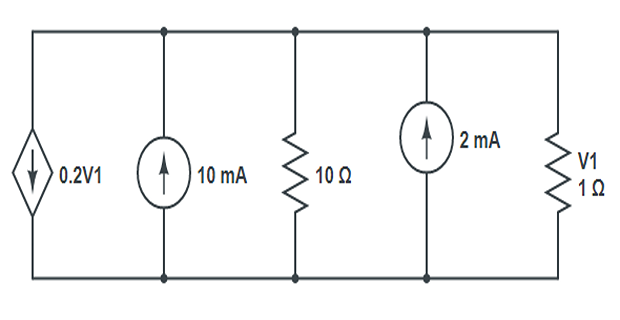
Solution-7
Applying KCL at node \[\begin{aligned} 0.2V_1 +(10\times 10^{-3})+\dfrac{V}{10} - (2\times 10^{-3})+\dfrac{V_1}{1}&=0 \\ \Rightarrow V_1 &= 9.23~\mathrm{mV} \end{aligned}\]
Problem-8
Find the current through the 5m\(\Omega\) resistor?
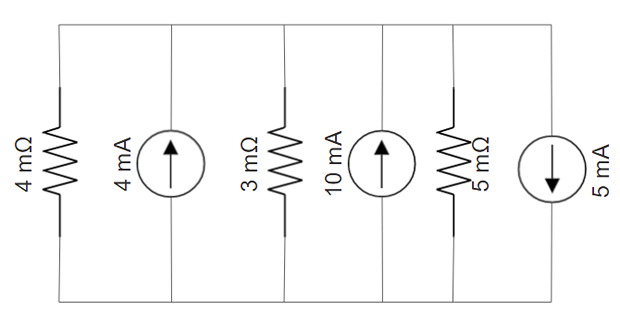
Solution-8
Applying KCL at node \[\begin{aligned} &\dfrac{V}{4m\Omega}-(4~\mathrm{mA})+\dfrac{V}{3~m\Omega}-(10~mA)+\dfrac{V}{5~m\Omega}-5~mA =0\\ &\Rightarrow V = 11.54\times 10^{-6}~\mathrm{V} \end{aligned}\]
Current through 5m\(\Omega\) resistor is \[I = \dfrac{11.54\times 10^{-6}}{5\times 10^{-3}} = 2.31\times 10^{-3}\]
Problem-9
Find the power supplied by the dependent source?
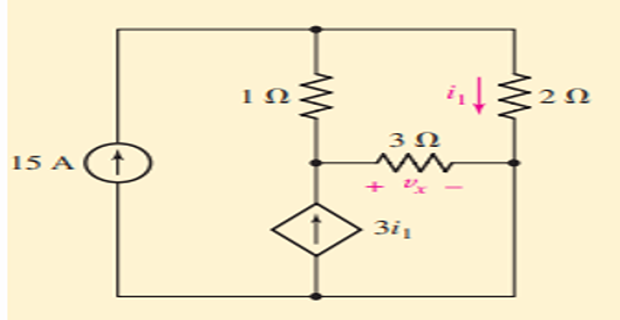
Solution-9
Applying KCL at node \(v_1\) \[\begin{aligned} -15+\dfrac{v_1-v_2}{1}+\dfrac{v_1}{2} & = 0 \end{aligned}\]
Applying KCL at node \(v_2\) \[-3i_1+\dfrac{v_2}{3}+\dfrac{v_2-v_1}{1} = 0\]

Also \[i_1 = \dfrac{v_1}{2}\]
On solving \[v_1 = -40~\mathrm{V} \quad v_2 = -75~\mathrm{V} \quad i_1 = -20~\mathrm{A}\]
Power supplied by dependent source \[P = (3i_1)(v_2) = 4.5~\mathrm{kW}\]
Problem-10
Determine the value of \(V1\) ?
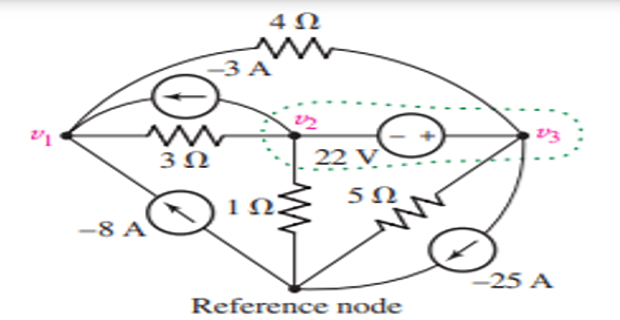
Solution-10
KCL at node \(v_1\) \[-(-8)-(-3)+\dfrac{v_1-v_2}{3}+\dfrac{v_1-v_3}{4}=0\]
Super-node analysis at \(v_2\)-\(v_3\) \[-3+\dfrac{v_2-v_1}{3}+\dfrac{v_2}{1}+\dfrac{v_3}{5}-25+\dfrac{v_3-v_1}{4}=0\]
Constraint equation at super-node \[v_3-v_2 = 22\]
On solving \[v_1 = 1.071~\mathrm{V} \quad v_2 =10.5 ~\mathrm{V} \quad v_3 = 32.5~\mathrm{V}\]