Solved Problems on Inductor Fundamentals

Solution-1

• Since \(i=\frac{1}{L} \int_{t_{0}}^{t} v(t) d t+i\left(t_{0}\right)\) and \(L=5 \mathrm{H}\), \[i=\frac{1}{5} \int_{0}^{t} 30 t^{2} d t+0=6 \times \frac{t^{3}}{3}=2 t^{3} \mathrm{~A}\]

• The power \(p=v i=60 t^{5}\), and the energy stored is then \[w=\int p d t=\int_{0}^{5} 60 t^{5} d t=\left.60 \frac{t^{6}}{6}\right|_{0} ^{5}=156.25 \mathrm{~kJ}\]

• Alternatively, we can obtain the energy stored \[\left.w\right|_{0} ^{5}=\frac{1}{2} L i^{2}(5)-\frac{1}{2} L i(0)=\frac{1}{2}(5)\left(2 \times 5^{3}\right)^{2}-0=156.25 \mathrm{~kJ}\]

Problem-2

• The current through 0.1 H inductor is \(i(t)=10t\cdot e^{-5t}\) A. Find the voltage across inductor and energy stored in it.

Solution-2

• Since \(v=L d i / d t\) and \(L=0.1 \mathrm{H}\), \[v=0.1 \frac{d}{d t}\left(10 t e^{-5 t}\right)=e^{-5 t}+t(-5) e^{-5 t}=e^{-5 t}(1-5 t) \mathrm{V}\]

• The energy stored is \[w=\frac{1}{2} L i^{2}=\frac{1}{2}(0.1) 100 t^{2} e^{-10 t}=5 t^{2} e^{-10 t} \mathrm{~J}\]

Problem-3

• The voltage across a 2 H inductor is known to be \(6cos5t\) V. Determine the resulting inductor current if \(i(t =-\pi/2)=1\) A.

Solution-3

• Current through inductor \[i(t)=\frac{1}{2} \int_{t_{0}}^{t} 6 \cos 5 t d t+i\left(t_{0}\right)\] or \[\begin{aligned} i(t) &=\frac{1}{2}\left(\frac{6}{5}\right) \sin 5 t-\frac{1}{2}\left(\frac{6}{5}\right) \sin 5 t_{0}+i\left(t_{0}\right) \\ &=0.6 \sin 5 t-0.6 \sin 5 t_{0}+i\left(t_{0}\right) \end{aligned}\]

• The first term indicates that the inductor current varies sinusoidally; the second and third terms together represent a constant which becomes known when the current is numerically specified at some instant of time.

• Using the fact that the current is \(1 \mathrm{~A}\) at \(t=-\pi / 2 \mathrm{~s}\), we identify \(t_{0}\) as \(-\pi / 2\) with \(i\left(t_{0}\right)=1\), and find that \[\begin{aligned} i(t)&=0.6 \sin 5 t-0.6 \sin (-2.5 \pi)+1\\ & = 0.6 \sin 5t + 1.6 \end{aligned}\]

Problem-4

• The terminal voltage of a 2 H inductor is \(v=10(1-t)\) V. Find the current flowing through it at \(t=4\) s and the energy stored in it at \(t=4\) s. Assume \(i(0) = 2\) A.

Solution-4

• Given data: \[\begin{aligned} L & = 2~\mathrm{A} \quad v(t) = 10(1-t)~\mathrm{V} \quad i(0) = 2~\mathrm{A} \end{aligned}\]

• Current expression: \[\begin{aligned} i(t) & = i(0) + \dfrac{1}{L} \int_{0}^{t} v(t)dt \\ & = 2+\dfrac{1}{2} \int_{0}^{t} (10-10t)dt \\ & = 2+5t-2.5t^2 \end{aligned}\]

• Value of current at 4 sec \[\begin{aligned} i(t)|_{t=4~\text{sec}} & = 2+20-40 = -18~\mathrm{A} \end{aligned}\]

• Energy: \[\begin{aligned} W|_{0}^{4~\text{sec}} & = \dfrac{1}{2} (L)\left[i^2(4)-i^2(0)\right]\\ & = 320~J \end{aligned}\]

Problem-5

• If the voltage waveform in the figure is applied to 10 mH inductor, find the inductor current \(i(t)\). Assume \(i(0)=0\) A.

  

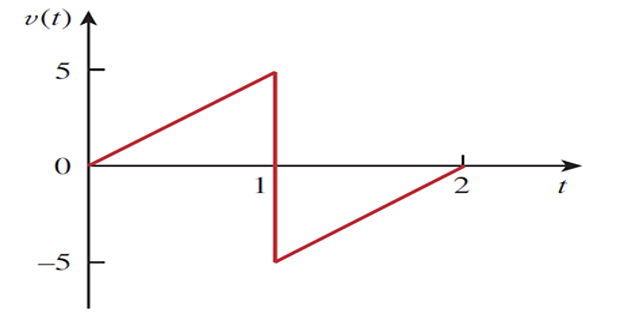
Solution-5

• Given data: \[\begin{aligned} i(0) & = 0~\mathrm{A} \quad L = 10~\mathrm{mH} \end{aligned}\]

• Voltage distribution:

  \[v(t) = \left\{\begin{array}{lr} 5t, & \text{for } 0<t<1\\ 5t-10, & \text{for } 1<t<2\\ 0, & \text{for } \text{elsewhere} \end{array}\right\}\]

• Current: \[i(t) = \left\{\begin{array}{lr} 250t^2, & \text{for } 0<t<1\\ 1000(1-t+0.25t^2), & \text{for } 1<t<2\\ 0, & \text{for } \text{elsewhere} \end{array}\right\}\]

Problem-6

• The current through 5 mH inductor is shown in fig. Determine the voltage across inductor at \(t=1,3,~ \text{and},~ 5\) ms.

  

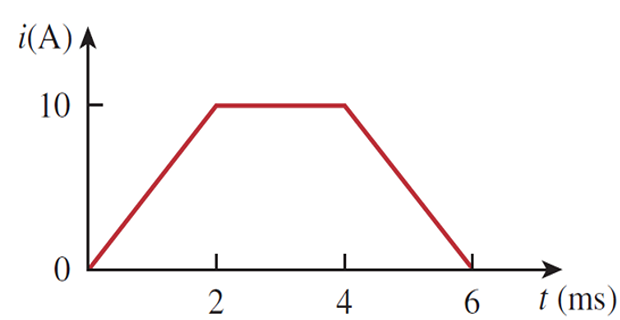
Solution-6

\[\begin{aligned} &\mathrm{v}=\mathrm{L} \frac{d i}{d t}=5 \times 10^{-3} \left\{\begin{array}{cl} 5, & 0<t<2 \mathrm{~ms} \\ 0, & 2<t<4 \mathrm{~ms} \\ -5, & 4<t<6 \mathrm{~ms} \end{array}=\left\{\begin{array}{cl} 25, & 0<t<2 \mathrm{~ms} \\ 0, & 2<t<4 \mathrm{~ms} \\ -25, & 4<t<6 \mathrm{~ms} \end{array}\right.\right. \\ &\\ &\text { At } \mathrm{t}=1 \mathrm{~ms}, \mathrm{v}=25 \mathrm{~V} \\ &\text { At } \mathrm{t}=3 \mathrm{~ms}, \mathrm{v}=0 \mathrm{~V}\\ &\text { At } \mathrm{t}=5 \mathrm{~ms}, \mathrm{v}=-25 \mathrm{~V} \end{aligned}\]

Problem-7

• Given the waveform of the current in a 3H inductor as shown in fig, determine the inductor voltage and sketch it.

  

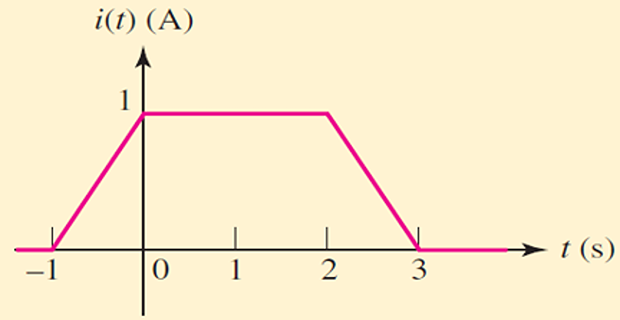
Solution-7

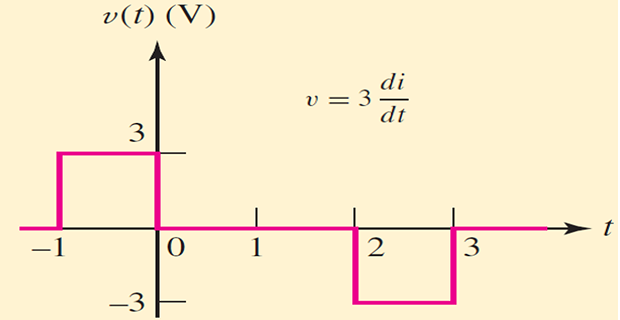
• For \(t<-1 \mathrm{~s}\) current is zero, the voltage is zero in this interval.

• The current then begins to increase at the linear rate of \(1 \mathrm{~A} / \mathrm{s}\), and thus a constant voltage of \(L d i / d t=3 \mathrm{~V}\) is produced.

• During the following \(2 \mathrm{~s}\) interval, the current is constant and the voltage is therefore zero.

• The final decrease of the current results in \(d i / d t=-1 \mathrm{~A} / \mathrm{s}\), yielding \(v=-3 \mathrm{~V}\). For \(t>3 \mathrm{~s}, i(t)\) is a constant (zero), so that \(v(t)=0\) for that interval.

Problem-8

• The voltage across 2 H is given by \[V_L=4.3t, \quad 0 \leq t \leq50~ms\].

  With the knowledge that \(i_L(-0.1)=100~\mu A\). Calculate the current (assuming it is defined consistent with the passive sign convention) at t equal to

  1. 0 ms

  2. 1.5 ms

  3. 45 ms

Solution-8

• Recall that the current flowing through an inductor is given by, \[\begin{aligned} i(t) &=\frac{1}{L} \int_{t_{0}}^{t} v(t) d t^{\prime}+i_{L}\left(t_{0}\right) \\ &=\frac{1}{2} \int_{-0.1}^{t} 4.3 t d t^{\prime}+100 \times 10^{-6} \\ &=\frac{4.3}{4}\left(t^{2}-0.01\right)++100 \times 10^{-6} \mathrm{~A} \quad 0 \leq t \leq 50 \mathrm{~ms} \end{aligned}\]

• \(t=0\), \[\begin{aligned} i(0) &=\frac{4.3}{4}\left(0^{2}-0.01\right)+100 \times 10^{-6} \\ &=-10.75 \times 10^{-3}+100 \times 10^{-6} \end{aligned}\] Thus, \[i(0)=-10.65 \mathrm{~mA}\]

Problem-9

• Determine the current flowing through a 6mH inductor if the voltage (defined such that it is consistent with the passive sign convention) is given by

  1. 5V;

  2. \(100 \sin(120 \pi t), \quad t \geq 0 ~\text{and}~ 0, ~t < 0\)

Solution-9

(a) \[i(t)=\frac{1}{L} \int_{0}^{t} v(t) d t^{\prime}+i_{L}(t)\] For \(v(t)=5 \mathrm{~V}\), \[\begin{aligned} i(t) &=\frac{1}{0.006} \int_{0}^{t} 5 d t^{\prime}+0 \\ &=\frac{1}{0.006}(5 t) \end{aligned}\] Thus, \[i(t)=833.33 t \mathrm{~A}\]

Problem-10

• A square waveform is applied across 1mH inductor. The current is a ……….wave of……..peak amplitude

  

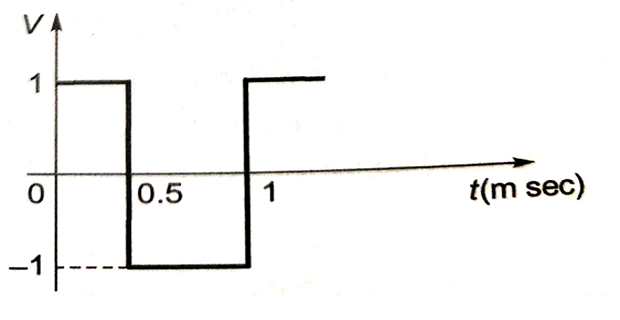
Solution-10

• Current: \[i_L = \dfrac{1}{L} \int V dt\] \[\begin{aligned} v(t) &=u(t)-2 u(t-0.5)+2 u(t-1)+\ldots \\ i_{L}(t) &=r(t)-2 r(t-0.5)+2 r(t-1)+\ldots \end{aligned}\] 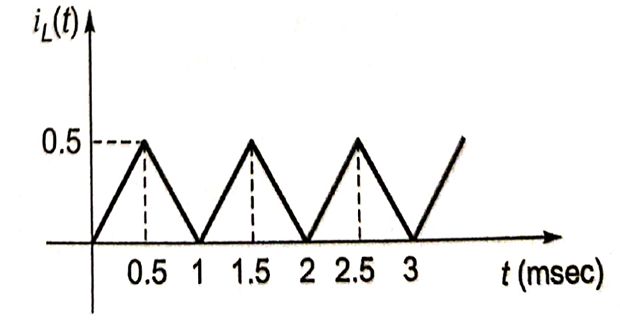\[I_p = 0.5~\mathrm{A}\]