Solved Problems on Capacitor Fundamentals

Demonstrative Video

Demonstrative Video

Problem 1

  • Calculate the charge stored in a 3 pF capacitor with 20 V across it. Also determine the energy stored in the capacitor.

Solution 1

  • Charge:
    \[ Q = C \cdot V = 3\times 10^{-12} \times 20 = 60~\mathrm{pC} \]
  • Energy:
    \[ W = \frac{1}{2} C \cdot V^2 = \frac{1}{2} \times 3\times 10^{-12} \times 400 = 600~\mathrm{pJ} \]

Problem 2

  • The voltage across a 5 \(\mu\)F capacitor is \(v(t) = 10\cos 6000t\) V. Calculate the current through it.

Solution 2

  • Current:
    \[ i(t) = C \frac{dv}{dt} = 5 \times 10^{-6} \cdot \frac{d}{dt}(10 \cos 6000t) = -0.3 \sin 6000t~\mathrm{A} \]

Problem-3

  • Determine the voltage across a 2 \(\mu\)F capacitor if the current through it is \(i(t)= 6e^{-3000t}\) mA. Assume that the initial capacitor voltage is zero.

.

Solution-3

\[\begin{aligned} &v=\frac{1}{C} \int_{0}^{t} i d t+v(0) \text { and } v(0)=0, \\ &v=\frac{1}{2 \times 10^{-6}} \int_{0}^{t} 6 e^{-3000 t} d t \cdot 10^{-3} \\ &=\left.\frac{3 \times 10^{3}}{-3000} e^{-3000 t}\right|_{0} ^{t}\\ &=\left(1-e^{-3000 t}\right) \mathrm{V} \end{aligned}\]

Problem-4

  • Determine the current through a 200 \(\mu\)F capacitor whose voltage is shown below

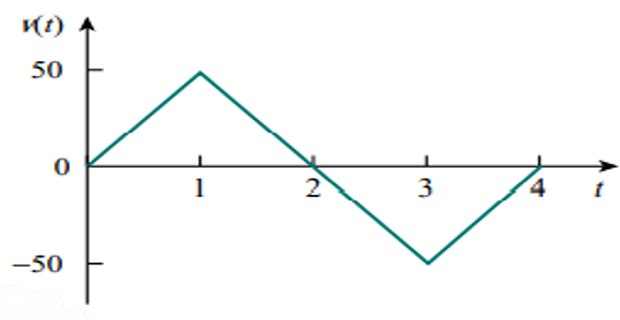
    image
    image

Solution-4

The voltage waveform

\[v(t)=\left\{\begin{array}{rl} 50 t \mathrm{~V} & 0<t<1 \\ 100-50 t \mathrm{~V} & 1<t<3 \\ -200+50 t \mathrm{~V} & 3<t<4 \\ 0 & \text { otherwise } \end{array}\right.\]
\[\begin{aligned} i(t) &=200 \times 10^{-6} \times\left\{\begin{array}{rl} 50 & 0<t \\ -50 & 1<t \\ 50 & 3<t \\ 0 & \text { otherwise } \end{array}\right. =\left\{\begin{array}{rl} 10 \mathrm{~mA} & 0<t<1 \\ -10 \mathrm{~mA} & 1<t<3 \\ 10 \mathrm{~mA} & 3<t<4 \\ 0 & \text { otherwise } \end{array}\right. \end{aligned}\]
image
image
to obtain , we take the derivative of and Since

Problem-5

  • Obtain the energy stored in each capacitor under the dc condition:

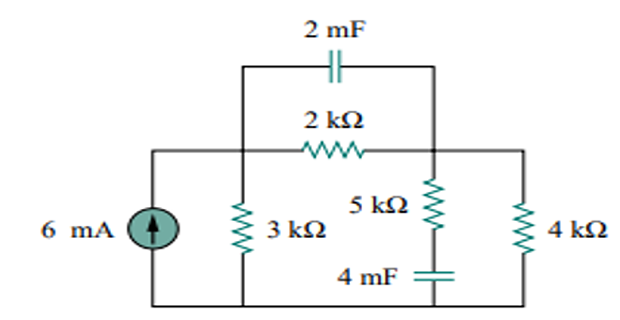
    image
    image

Solution-5

  • Under dc condition, replace each capacitor with OC.

  • \[\begin{aligned} i = \dfrac{3}{3+2+4}(6~\mathrm{mA}) = 2~\mathrm{mA} \end{aligned}\]
    resistors and The current through the series combination of the

  • Voltages across the capacitors:

    \[\begin{aligned} v_1 & = 2000i = 4~V \qquad v_2 = 4000i = 8~V \end{aligned}\]

  • Energy stored:

    \[\begin{aligned} &w_{1}=\frac{1}{2} C_{1} v_{1}^{2}=\frac{1}{2}\left(2 \times 10^{-3}\right)(4)^{2}=16 \mathrm{~mJ} \\ &w_{2}=\frac{1}{2} C_{2} v_{2}^{2}=\frac{1}{2}\left(4 \times 10^{-3}\right)(8)^{2}=128 \mathrm{~mJ} \end{aligned}\]

Problem-6

  • Find the equivalent capacitance between the terminals:

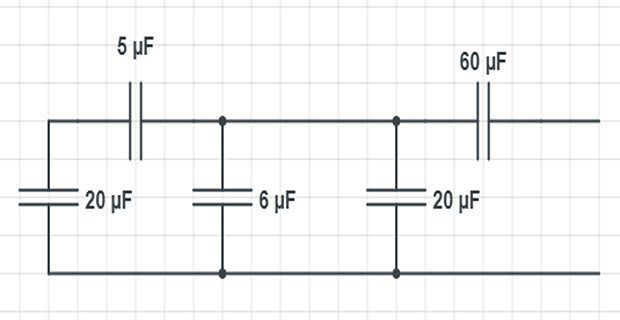
    image
    image

Solution-6

  • \[\frac{20 \times 5}{20+5}=4 \mu \mathrm{F}\]
    and Equivalent capacitance of series capacitors
  • \[4+6+20=30 \mu \mathrm{F}\]
    and 20- capacitor is in parallel with the 6- This 4-

  • This \(30-\mu \mathrm{F}\) capacitor is in series with the \(60-\mu \mathrm{F}\) capacitor.

  • \[C_{\mathrm{eq}}=\frac{30 \times 60}{30+60}=20 \mu \mathrm{F}\]
    Hence, the equivalent capacitance for the entire circuit is

Problem-7

  • Find the voltage across each capacitors:

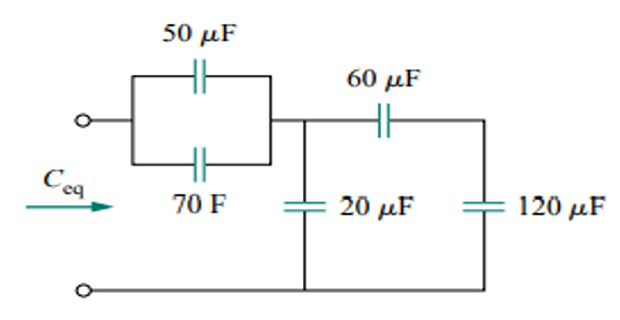
    image
    image

Solution-7

  • We first find the equivalent capacitance \(C_{\mathrm{eq}}\).

  • The two parallel capacitors can be combined to get \(40+20=60 \mathrm{mF}\).

  • \[C_{\mathrm{eq}}=\frac{1}{\frac{1}{60}+\frac{1}{30}+\frac{1}{20}} \mathrm{mF}=10 \mathrm{mF}\]
    and is in series with the This

  • The total charge is \(q=C_{\mathrm{eq}} v=10 \times 10^{-3} \times 30=0.3 \mathrm{C}\)

  • \[v_{1}=\frac{q}{C_{1}}=\frac{0.3}{20 \times 10^{-3}}=15 \mathrm{~V} \quad v_{2}=\frac{q}{C_{2}}=\frac{0.3}{30 \times 10^{-3}}=10 \mathrm{~V}\]
    source. Therefore, and 30 -mF capacitors, because they are in series with the This is the charge on the
  • Finally
    \[\begin{aligned} \text{KVL}~&v_{3}=30-v_{1}-v_{2}=5 \mathrm{~V} \\ \text{or}~&v_{3}=\frac{q}{60 \mathrm{mF}}=\frac{0.3}{60 \times 10^{-3}}=5 \mathrm{~V} \end{aligned}\]

Problem-8

  • Assuming the capacitors are initially uncharged, find \(v_0\)

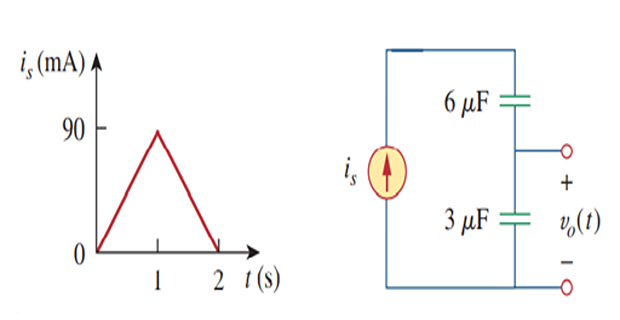
    image
    image

Solution-8

\[\mathrm{v}_{\mathrm{o}}=\frac{1}{\mathrm{C}} \int_{\mathrm{o}}^{\mathrm{t}} \mathrm{idt}+\mathrm{i}(0)\]
For \(0<\mathrm{t}<1, \quad ~~\mathrm{i}=90 \mathrm{t} \mathrm{mA}\),
\[\begin{aligned} &v_{o}=\frac{10^{-3}}{3 \times 10^{-6}} \int_{o}^{t} 90 t d t+0=15 t^{2} k V \\ &\mathrm{v}_{\mathrm{o}}(1)=15 \mathrm{kV} \end{aligned}\]

For

\(1<\mathrm{t}<2, \mathrm{i}=(180-90 \mathrm{t}) \mathrm{mA}\),
\[\begin{aligned} & \mathrm{v}_{\mathrm{o}}=\frac{10^{-3}}{3 \times 10^{-6}} \int_{1}^{t}(180-90 t) d t+v_{o}(1) \\ =&\left[60 \mathrm{t}-15 \mathrm{t}^{2}\right]_{1}^{t}+15 \mathrm{kV} \\ =&\left[60 \mathrm{t}-15 \mathrm{t}^{2}-(60-15)+15\right] \mathrm{kV}=\left[60 \mathrm{t}-15 \mathrm{t}^{2}-30\right] \mathrm{kV} \\ & v_{o}(t)=\left[\begin{array}{ll} 15 t^{2} k V, & 0<t<1 \\ {\left[60 t-15 t^{2}-30\right] k V,} & 1<t<2 \end{array}\right. \end{aligned}\]

Problem-9

If \(v_0=0\), find \(v(t),~i_1(t) ~\text{and}~ i_2(t)\)

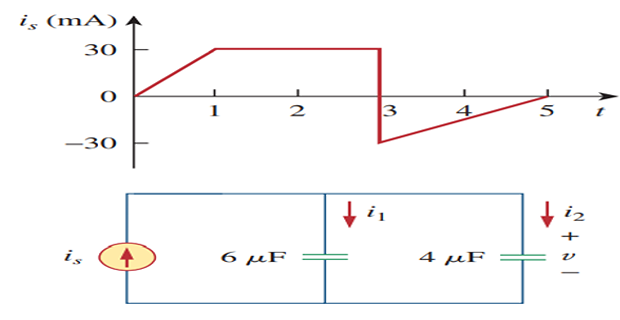
image
image

Solution-9

\[\begin{aligned} &i_{s}(t)=\left[\begin{array}{ll} 30 \operatorname{tm} A, & 0<t<1 \\ 30 m A, & 1<t<3 \\ -75+15 t, & 3<t<5 \end{array}\right. \\ &\mathrm{C}_{\mathrm{eq}}=4+6=10 \mu \mathrm{F} \\ &\mathrm{v}=\frac{1}{\mathrm{C}_{\mathrm{eq}}} \int_{\mathrm{o}}^{\mathrm{t}} \mathrm{idt}+\mathrm{v}(0) \end{aligned}\]

For

\(0<\mathrm{t}<1\),
\[v=\frac{10^{-3}}{10 x 10^{-6}} \int_{o}^{t} 30 t \mathrm{dt}+0=1.5 \mathrm{t}^{2} \mathrm{kV}\]
For \(1<\mathrm{t}<3\),
\[\begin{gathered} v=\frac{10^{3}}{10} \int_{1}^{t} 20 d t+v(1)=[3(t-1)+1.5] \mathrm{kV} \\ =[3 t-1.5] \mathrm{kV} \end{gathered}\]

For

\(3<t<5\),
\[\begin{aligned} v &=\frac{10^{3}}{10} \int_{3}^{t} 15(t-5) d t+v(3) \\ &=\left.\left[1.5 \frac{t^{2}}{2}-7.5 t\right]\right|_{3} ^{t}+7.5 k V=\left[0.75 t^{2}-7.5 t+23.25\right] k V \end{aligned}\]

\(v(t)=\left[\begin{array}{lc}1.5 t^{2} k V, & 0<t<1 s \\ {[3 t-1.5] k V,} & 1<t<3 s \\ {\left[0.75 t^{2}-7.5 t+23.251 k V,\right.} & 3<t<5 s\end{array}\right.\)

\(i_{1}=C_{1} \frac{d v}{d t}=6 \times 10^{-6} \frac{d v}{d t} \\ i_{1}=\left[\begin{array}{ll}18 t~\mathrm{mA}, & 0<t<1 s \\ 18~\mathrm{mA}, & 1<t<3 s \\ {[9 t-45] ~\mathrm{mA},} & 3<t<5 s\end{array}\right.\)
\(i_{2}=C_{2} \frac{d v}{d t}=4 \times 10^{-6} \frac{d v}{d t} \\ i_{2}=\left[\begin{array}{lc}12 t~\mathrm{mA}, & 0<t<1 s \\ 12 ~\mathrm{mA}, & 1<t<3 s \\ {[6 t-30] ~\mathrm{mA},} & 3<t<5 s\end{array}\right.\)