Solved Problems on Thevenin's Theorem

Demonstrative Video

Problem-1

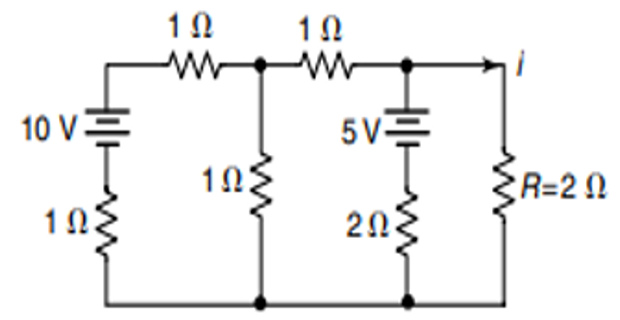
image

Solution-1

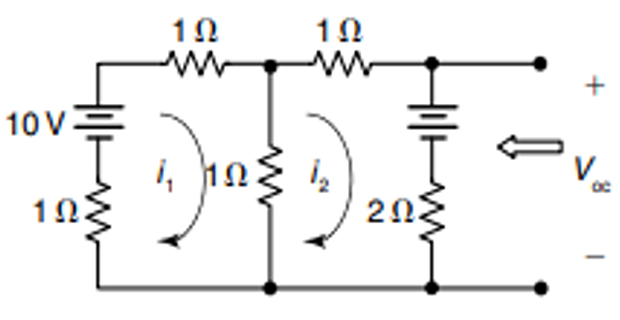
image
  • \[\begin{aligned} 3i_1-i_2&=10\\ -i_1+4i_2&=-5 \end{aligned}\]
    Applying mesh analysis
  • \[\begin{aligned} i_1&=5/11, \quad i_2 = -5/11 \end{aligned}\]
    On solving:
  • \[\begin{aligned} V_{TH}&=(5+2i_2)=(5-\dfrac{10}{11})=\dfrac{45}{11}~\mathrm{V} \end{aligned}\]
    Thevenin or
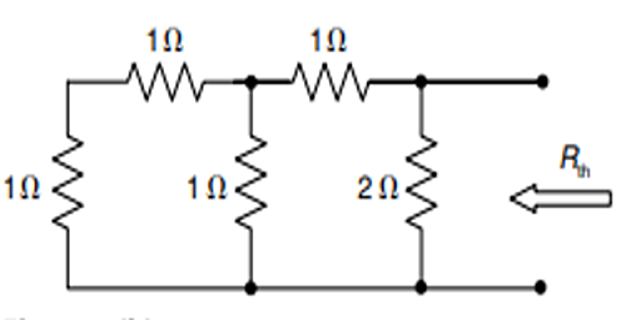
image

  • Equivalent resistance, \(R_{\text {TH }}=\dfrac{\dfrac{5}{3} \times 2}{5 / 3+2}=\dfrac{10}{11} \Omega\)

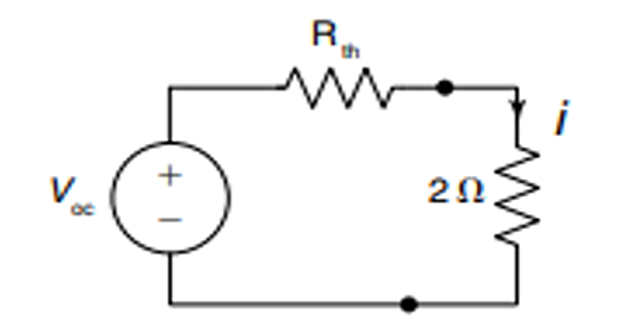
  • Load current is, \(i=\dfrac{V_{o c}}{R_{\mathrm{TH}}+2}=\dfrac{45 / 11}{10 / 11}=\dfrac{45}{32}=1.40625 \mathrm{~A}\)

    image

Problem-2

  • Find the current through 15 \(\Omega\) using the Thevenin’s Theorem?

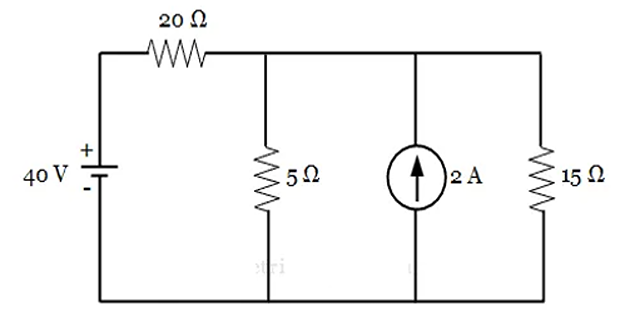
image

Solution-2

\[\begin{gathered} 25 I=30 \\ I=1.2 \mathrm{~A} \\ V_{T H}=10+\left(5\times1.2\right)=16 v \end{gathered}\]
Applying KVL
\[\begin{aligned} &R_{T H}=\frac{5 \times 20}{5+20}=4 \Omega \\ &I_{L}=\frac{V_{T H}}{R_{T H}+R_{L}}=\frac{16}{4+15}=0.842 A \end{aligned}\]

Problem-3

  • Find the Thevenin’s volatge and resistance at terminals 1-2?

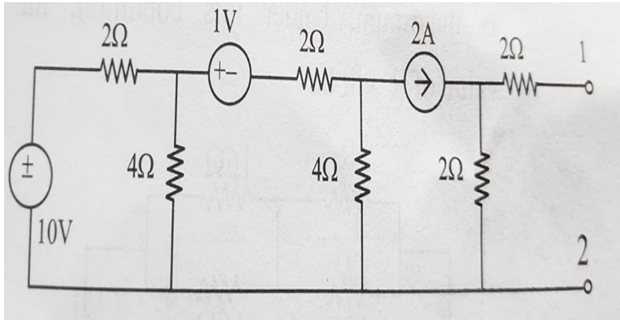
image

Solution-3


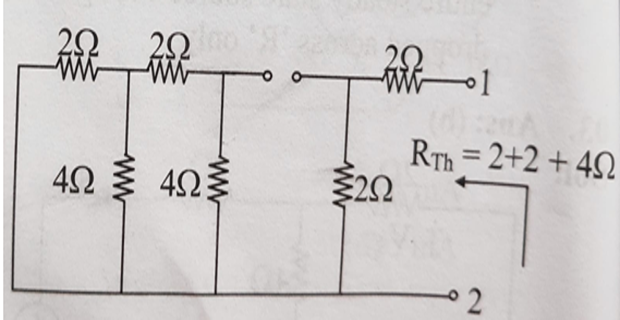
image

  • SC the voltage source and OC the current source \(R_{TH}=4\Omega\)

  • Thevenin’s voltage \(V_{TH}=4\mathrm{V}\)

Problem-4

  • Find the Thevenin’s resistance at terminals P-Q?

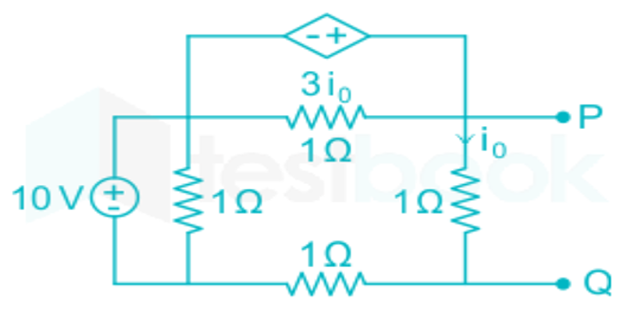
image

Solution-4

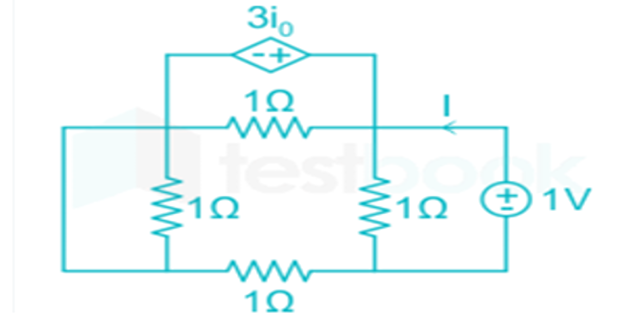
image

  • Connecting 1V source by SC indep. voltage source \(I=1\mathrm{A}\)

  • \(R_{TH}=V/I=1\Omega\)

Problem-5

  • Find the current flowing through A-B using Thevenin’s theorem?

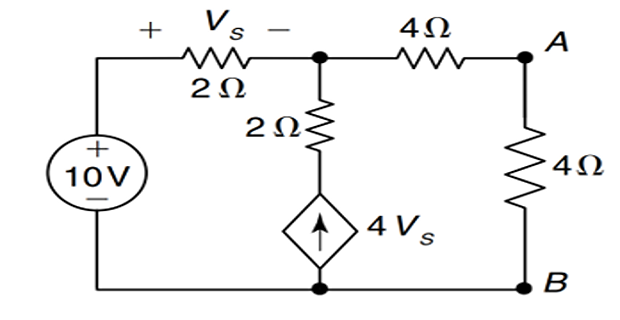
image

Solution-5

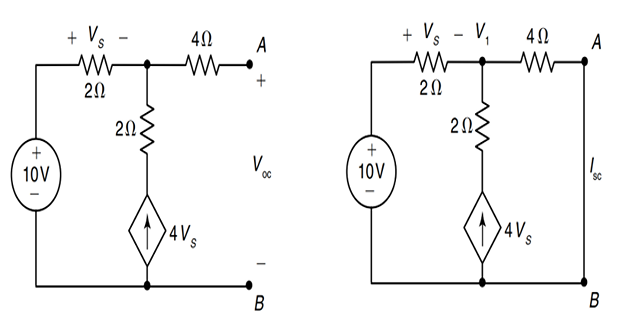
image
  • \[\frac{V_{\mathrm{oc}}-10}{2}=4 v_{s}=4\left(10-V_{\mathrm{oc}}\right) \Rightarrow V_{\mathrm{oc}}=10 \mathrm{~V}\]
    , resistor by Open-circuiting the
  • \[\begin{aligned} &\frac{V_{1}-10}{2}+\frac{V_{1}}{4}=4 v_{s}=4\left(10-V_{1}\right) \\ &\quad V_{1}=\frac{180}{19}=9 \cdot 47 \mathrm{~V} \\ &\therefore \quad I_{\mathrm{sc}}=\frac{9 \cdot 47}{4}=2 \cdot 368 \mathrm{~A} \\ &\therefore \quad R_{\mathrm{th}}=\frac{V_{\mathrm{th}}}{I_{\mathrm{sc}}}=4 \cdot 22 \Omega \end{aligned}\]
    SC the terminals AB

Problem-6

  • Find the Thevenin’s equivalence at terminals a-b?

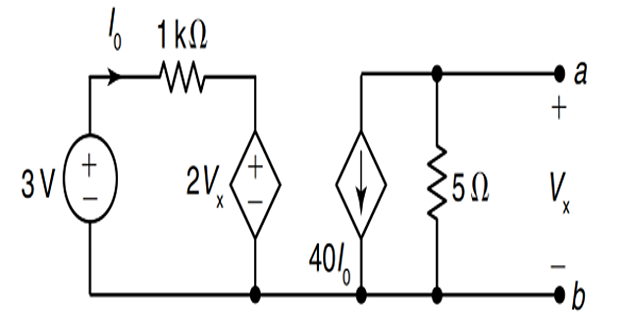
image

Solution-6

  • \[1 \times 10^{3} \times I+\frac{V_{0}}{10^{4}}=10 \times 10^{-3}\]
    By KVL for LHS loop,
  • \[V_{0}=30 \times 10^{3} \times(-75 I)=-225 \times 10^{4} I\]
    In the RHS loop, the dependent current source will circulate in the resistor. By KVL,
  • \[\begin{aligned} &\Rightarrow 1 \times 10^{3} \times\left(-\frac{V_{0}}{225 \times 10^{4}}\right)+\frac{V_{0}}{10^{4}}=10 \times 10^{-3} \\ &\Rightarrow-4.44 \times 10^{-4} V_{0}+1 \times 10^{-4} V_{0}=10 \times 10^{-3} \\ &\Rightarrow V_{0}=-\frac{10 \times 10^{-3}}{3.44 \times 10^{-4}}=-29 \mathrm{~V} \end{aligned}\]
    from (ii) in (i), we get, Substituting the value of
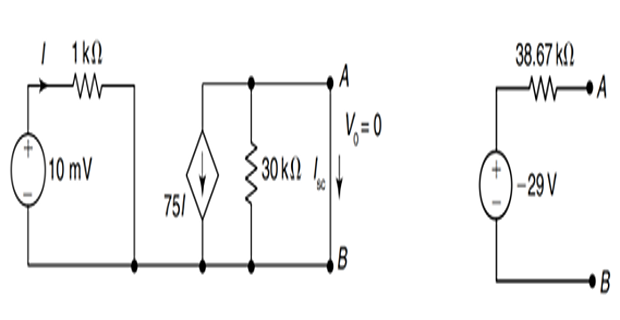
image
  • \[1 \times 10^{3} \times I+0=10 \times 10^{-3} \Rightarrow I=1 \times 10^{-5} \mathrm{~A}\]
    , we get by KVL to LHS loop, and Now, SC the terminals

  • Also, from RHS loop on the short circuit, \(I_{\mathrm{sc}}=-75 I=-75 \times 1 \times 10^{-5}=-75 \times 10^{-5} \mathrm{~A}\)

  • \[Z_{\mathrm{th}}=\frac{V_{\mathrm{oc}}}{I_{\mathrm{sc}}}=\frac{-29}{-75 \times 10^{-5}}=38.67 \mathrm{k} \Omega\]
    Thus, the Thevenin equivalent impedance is given as

Problem-7

  • Find the Thevenin’s resistance at terminals C-D?

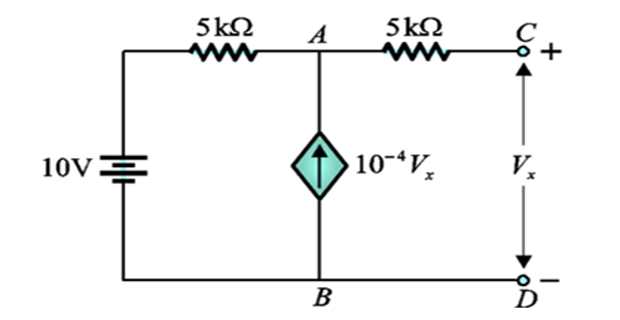
image

Solution-7

  • SC the voltage source and connect \(V_x=1\mathrm{V}\)

  • \(R_{TH}=V_x/I_x = 20~k\Omega\)

Problem-8

  • Find the Thevenin’s equivalence at terminals a-b?

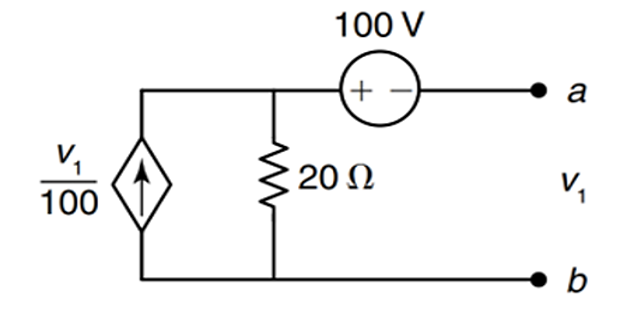
image

Solution-8

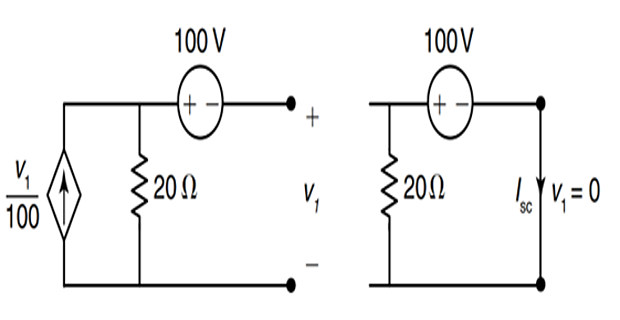
image

  • \(I_{sc}=100/20=5\Omega\)

  • \[-\frac{v_{oc}}{100}+\frac{100+v_{oc}}{20}=0 \Rightarrow-v_{oc}+500+5 v_{o c}=0 \Rightarrow v_{o c}=-125 \mathrm{~V}\]
    Applying KCL in open circuit

  • \(R_{TH}=\dfrac{V_{oc}}{I_{sc}}= 25\Omega\)