Solved Problems on Kirchhoff's Voltage and Current Laws (KVL & KCL)
Demonstrative Video
Problem-1
Find \(v_0\) and \(i_0\) in the given circuit?
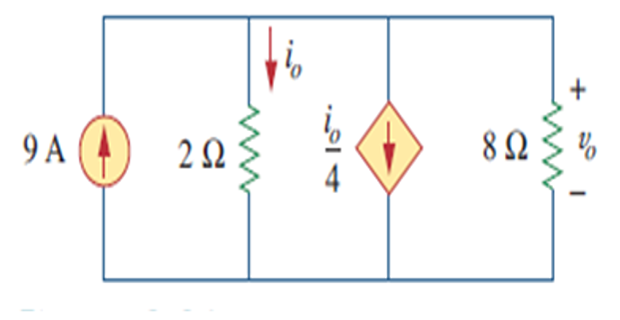
Solution-1
KCL at first node \(A\) : \(9 = i_0 + i_1 \Rightarrow i_1 = 9-i_0\)
KCL at second node \(B\) : \(i_1 = \dfrac{i_0}{4}+i_2 \Rightarrow i_1 = \dfrac{i_0}{4}+\dfrac{v_0}{8}\)
substituting the first in second, we get \[\begin{aligned} 9-i_0 & = \dfrac{i_0}{4}+\dfrac{v_0}{8} \\ \Rightarrow 9-\dfrac{v_0}{8} & = \dfrac{5i_0}{4} \end{aligned}\]
Also, \(V_A = V_B = V_0 = 2i_0\)
Therefore, \[\begin{aligned} 9-\dfrac{v_0}{8} & = \dfrac{5i_0}{4} \\ 9-\dfrac{i_0}{4} & = \dfrac{5i_0}{4} \\ i_0 & = 6~\mathrm{A} \\ v_0 & = 2i_0 = 12~\mathrm{V} \end{aligned}\]
Problem-2
Obtain the current \(I\) in the network?
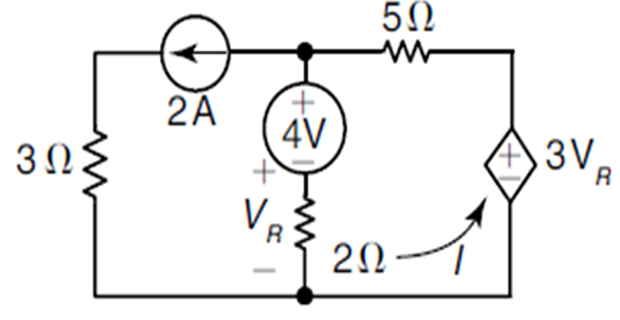
Solution-2
Applying KVL in Loop-2 \[\begin{aligned} 3V_R - 5I-4-V_R & = 0\\ \Rightarrow 2V_R & = 5I+4 \end{aligned}\]
Applying KCL at Node-A \(I_1 = I-2\)
Now, \(V_R = 2I_1 = 2I-4\)
On substitution \[\begin{aligned} 2(2I-4) & = 5I+4\\ \Rightarrow I & = -12~\mathrm{A} \end{aligned}\]
Problem-3
Obtain the current \(i\) in the network?
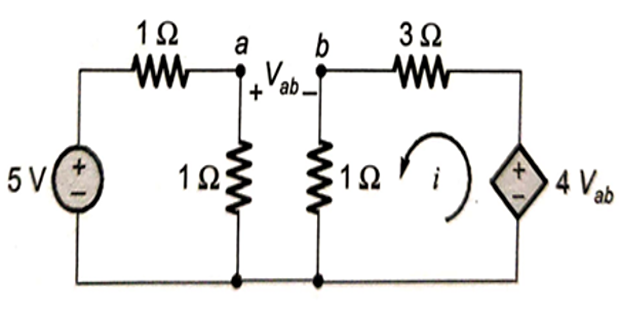
Solution-3
KVL in first loop gives \(5 = 2I_1 \Rightarrow I_1 = 2.5~\mathrm{A}\)
\(V_a = I_1=2.5~\mathrm{V}\)
KVL in second loop \(4V_{ab} = 4i \Rightarrow i = V_{ab}\)
\(V_b = i\)
\(V_{ab} = V_a - V_b = 2.5 - i = i\)
Hence, \(i = 1.25~\mathrm{A}\)
Problem-4
Determine the following in the circuit
\(V_{R2}\)
\(V_2\) if \(V_{R1}=1\)
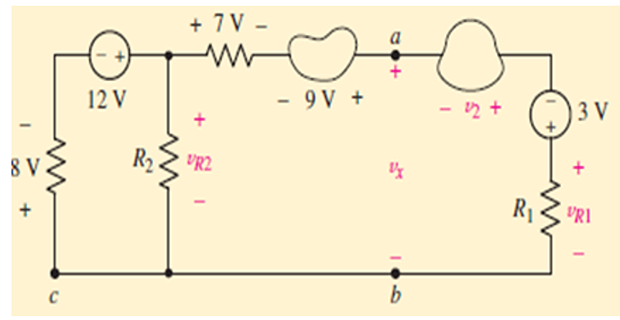
Solution-4
KVL in first loop gives \[-8+12-V_{R2} = 0 \Rightarrow V_{R2} = 4~\mathrm{V}\]
Also applying KVL \[V_{R2}-7+9-v_{x} =0 \Rightarrow v_x = 6~\mathrm{V}\]
Again applying KVL \[v_x +v_2+3-v_{R1}=0 \Rightarrow v_2 = -v_x-3+v_{R1} = -8~\mathrm{V}\]
Problem-5
The voltage source in the given circuit has a current of 1A flowing out of its positive terminal into resistor \(R_1\) .Calculate the current labelled \(i_2\).
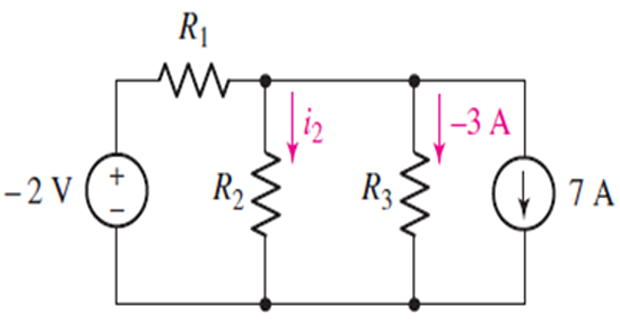
Solution-5
\[\begin{aligned} 1 &= i_2 -3 +7 \\ \Rightarrow i_2& = -3~\mathrm{A} \end{aligned}\]
Problem-6
Determine the value of the voltage \(v\) ?
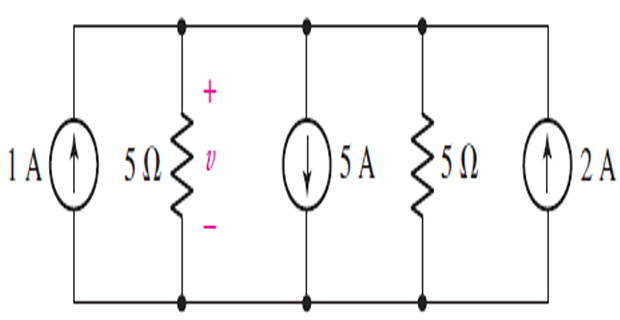
Solution-6
Applying KCL
\[\begin{aligned} 1+2&=\dfrac{v}{5}+5+\dfrac{v}{5} \\ -2 & = \dfrac{2v}{5}\\ v & = -5~\mathrm{V} \end{aligned}\]
Problem-7
Find the current \(i_x\) in the circuit shown?
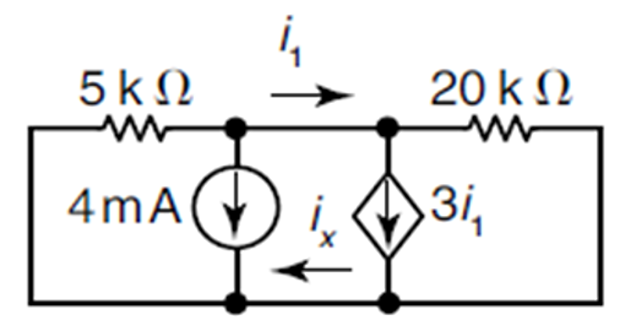
Solution-7
Applying KCL at three nodes \[\begin{aligned} 4\mathrm{mA}+3i_1+\dfrac{V}{5~k\Omega}+\dfrac{V}{20~k\Omega}&=0\\ i_1 & = 3i_1+\dfrac{V}{20~k\Omega}\\ 3i_1+\dfrac{V}{20~k\Omega} & = i_x \end{aligned}\]
Solving the first two and then putting in third, we get \[i_x = 0.57~\mathrm{A}\]
Problem-8
For the given circuit, use the KVL to find the branch voltages \(V_1\) to \(V_4\)?
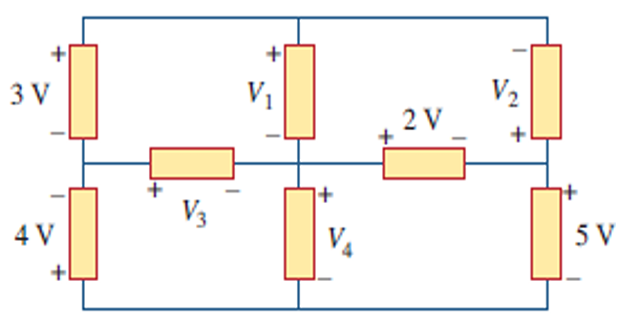
Solution-8
Applying KVL in 4 loops \[\begin{aligned} 3-V_1+V_3&=0\\ V_1+V_2+2&=0\\ -4-V_3-V_4&=0\\ V_4-2-5&=0 \end{aligned}\]
\(V_4=7\mathrm{V}~V_3=-11\mathrm{V}~V_1=-8\mathrm{V}~V_2=6\mathrm{V}\)
Problem-9
Determine the value of \(v_x\) labelled in the circuit?
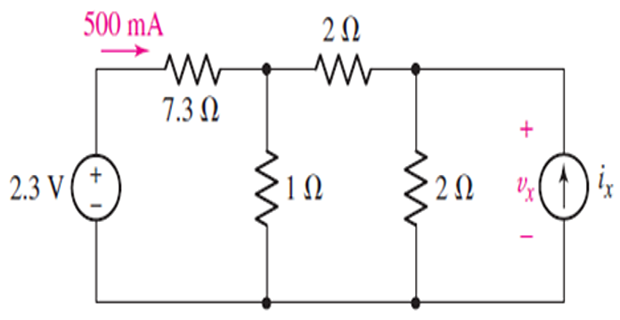
Solution-9
Voltage at first node \(2.3-500mA\times 7.3=-1.35\mathrm{V}\)
Applying KCL at first node \(0.5+1.35=I_2\)
Therefore \(v_x = -1.35-1.85\times 2=-5.05\mathrm{V}\)
Problem-10
The current \(I_x\) in the circuit given ?
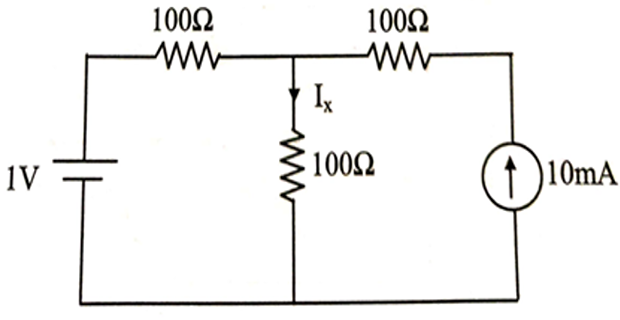
Solution-10
Applying KCL at node \[\dfrac{V-1}{100}+\dfrac{V}{100} = 10~\mathrm{mA}\]
Then, \[I_x = \dfrac{V}{100}\]
\(I_x = 10~\mathrm{mA}\)