Superposition & Source Transformation Theorems

Demonstrative Video

Introduction

  • Electric circuits has led to an evolution from simple to complex circuits.

  • To handle the complexity, engineers over the years have developed some theorems to simplify circuit analysis.

  • Such theorems include

    1. Thevenin’s and Norton’s

    2. Superposition

    3. Source transformation

    4. Maximum power transfer

  • Since these theorems are applicable to linear circuits, we first discuss the concept of circuit linearity

Linearity Property & Linear Circuits

  • Linearity : property of an element describing a linear relationship between cause and effect.

  • combination of homogeneity (scaling) + additivity property

  • \[\text{Input (excitation)} \times K (\text{constant}) \Rightarrow \text{Output (response)} \times K\]
    Homogeneity
  • \[V = IR \Rightarrow V\times K = K\times IR\]
    Ohm’s law
  • \[\begin{aligned} v_1 & = i_1\cdot R\\ v_2 & = i_2 \cdot R\\ v&=\left(i_{1}+i_{2}\right) R=i_{1} R+i_{2} R=v_{1}+v_{2} \end{aligned}\]
    Additivity :

  • Linear circuit : output is linearly related (or directly proportional) to its input.

  • A resistor is a linear element because the voltage-current relationship satisfies both the homogeneity and the additivity properties

  • A linear circuit consists of only linear elements, linear dependent sources, and independent sources

  • Note: \(p=i^{2} R=v^{2} / R\) (making it a quadratic function rather than a linear one), the relationship between power and voltage (or current) is nonlinear.

  • Therefore, the theorems are not applicable to power.

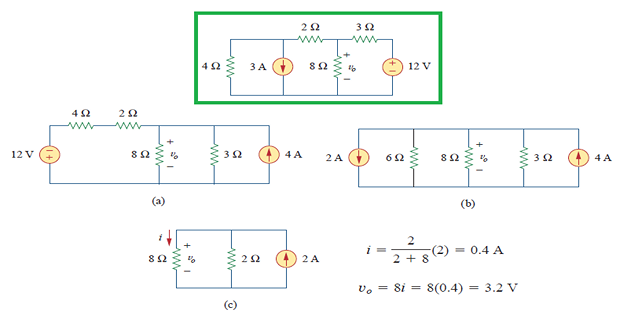
Superposition

  • The idea of superposition rests on the linearity property

  • The superposition principle states that the voltage across (or current through) an element in a linear circuit is the algebraic sum of the voltages across (or currents through) that element due to each independent source acting alone.

  • Helps to analyze a linear circuit with more than one independent source by calculating the contribution of each independent source separately

  • Two things should be kept in mind:

    1. consider one independent source at a time while all other independent sources are turned off.

      • replace every voltage source by 0 V (or a short circuit)

      • every current source by 0 A (or an open circuit)

    2. Dependent sources are left intact because they are controlled by circuit variables.

  • Steps to Apply Superposition Principle :

    1. Turn off all independent sources except one source. Find the output (voltage or current) due to that active source using the any technique

    2. Repeat step 1 for each of the other independent sources

    3. Find the total contribution by adding algebraically all the contributions due to the independent sources.

  • Note: superposition is based on linearity so not applicable to the effect on power due to each source.

  • If the power value is needed, the current through (or voltage across) the element must be calculated first using superposition.

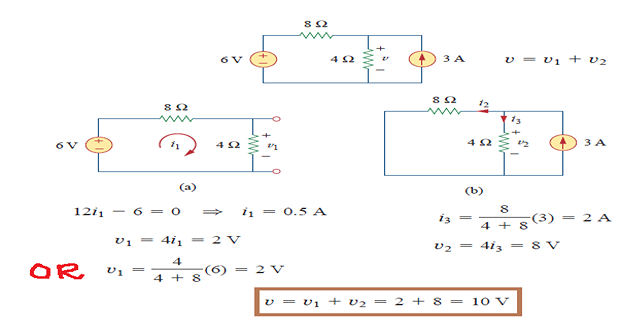
image

Source Transformation

  • Based on concept of equivalence recalling that an equivalent circuit is one whose v-i characteristics are identical with the original circuit.

  • Source transformation is the process of replacing a \(V_s\) in series with \(R\) by \(I_s\) in parallel with \(R\), or vice versa.

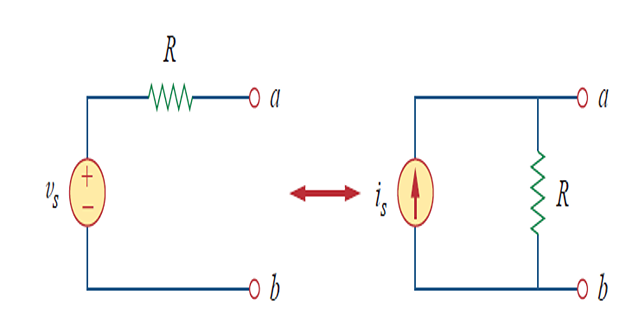
    image

  • Two circuits have same voltage-current relation at terminals a-b

  • If the sources are turned off, the equivalent resistance at terminals a-b in both circuits is R.

  • \[v_{s}=i_{s} R \quad \text { or } \quad i_{s}=\frac{v_{s}}{R}\]
    source transformation requires

  • Also applies to dependent sources, provided we carefully handle the dependent variable

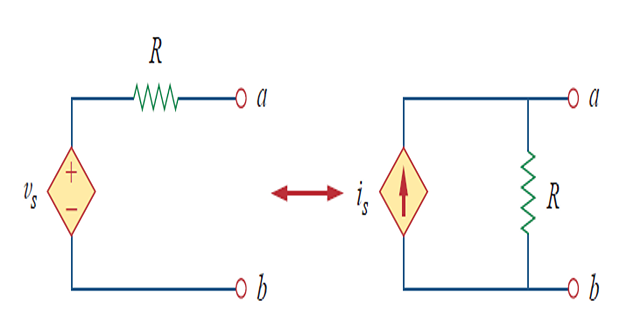
    image

  • Does not affect the remaining part of the circuit

  • Following points in mind when dealing with source transformation

    • arrow of the \(I_s\) is directed toward the positive terminal of \(V_s\)

    • not possible when \(R=0\), which is the case with an ideal voltage source

    • Similarly, an ideal current source \(R=\infty\) with cannot be replaced by a finite voltage source

image