Sinusoidal Steady-State Analysis
Demonstrative Video
Steady-State Analysis Methodology
Forced or steady-state response of circuits to sinusoidal inputs can be obtained by using phasor.
Covered Ohm’s and Kirchhoff’s laws for ac circuits.
Nodal analysis, mesh analysis, Thevenin’s theorem, Norton’s theorem, superposition, and source transformations in ac circuits.
Techniques already introduced for dc circuits.
Illustration with examples.

Nodal Analysis
Find ixix using Nodal analysis?
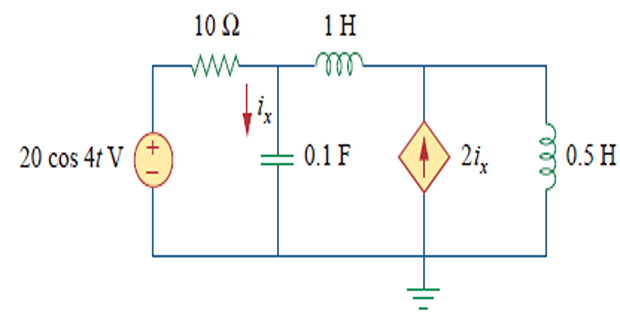
20cos4t⇒20∠0∘ω=4 rad/s1H⇒jωL=j40.5H⇒jωL=j20.1 F⇒1jωC=−j2.5
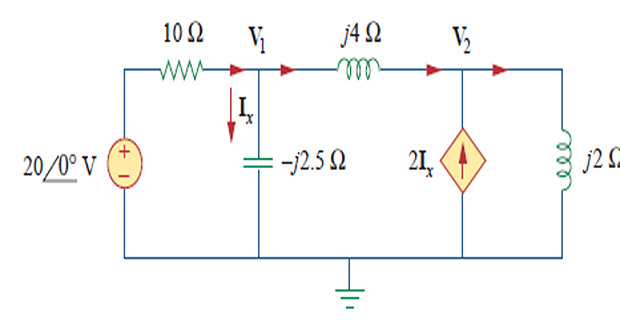
20−V110=V1−j2.5+V1−V2j4⇒(1+j1.5)V1+j2.5V2=202Ix+V1−V2j4=V2j2⇒2V1−j2.5+V1−V2j4=V2j2⇒11V1+15V2=0Ix=V1/−j2.5[1+j1.5j2.51115][V1V2]=[200]⇒V1=18.97∠18.43∘VV2=13.91∠198.3∘VIx=V1−j2.5=18.97∠18.43∘2.5∠−90∘=7.59∠108.4∘A⇒ix=7.59cos(4t+108.4∘)A
Super-Nodal Analysis
Compute V1 and V2 ?
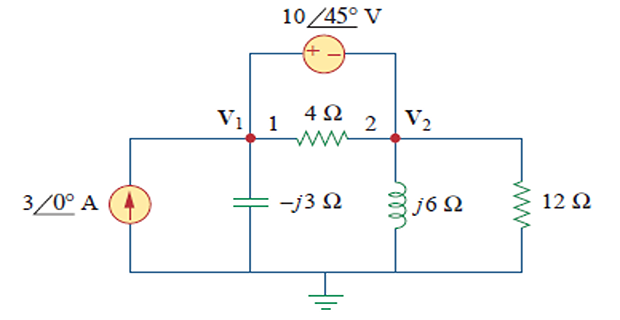
3=V1−j3+V2j6+V212V1=V2+10∠45∘
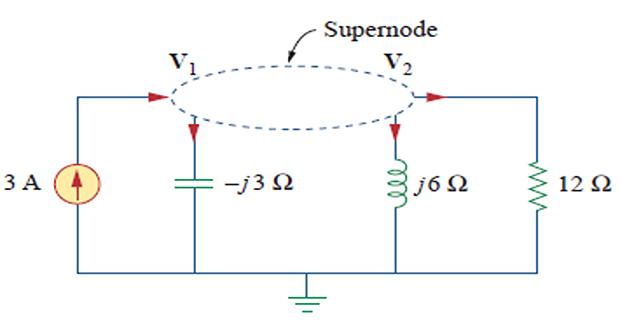
V1=25.78∠−70.48∘VV2=31.41∠−87.18∘V
Mesh Analysis
Determine the current I0 using
Mesh analysis ?
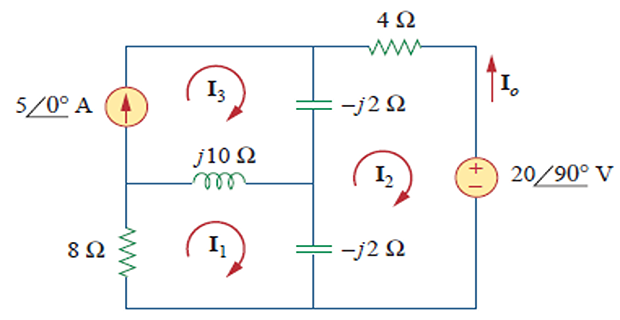
(8+j10−j2)I1−(−j2)I2−j10I3=0(4−j2−j2)I2−(−j2)I1−(−j2)I3+20∠90∘=0 For mesh 3,I3=5. (8+j8)I1+j2I2=j50j2I1+(4−j4)I2=−j20−j10[8+j8j2j24−j4][I1I2]=[j50−j30]I2=6.12∠−35.22∘AIo=−I2=6.12∠144.78∘A
Super-Mesh Analysis
Determine V0 using mesh
analysis?
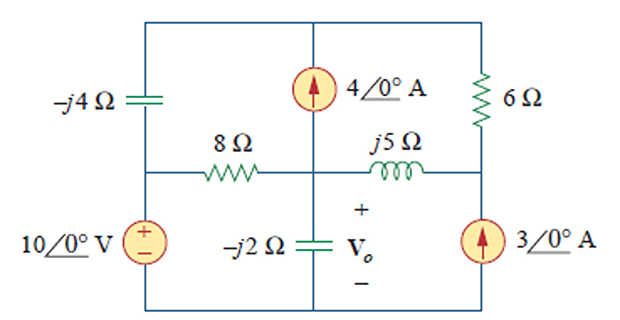
−10+(8−j2)I1−(−j2)I2−8I3=0I2=−3(8−j4)I3−8I1+(6+j5)I4−j5I2=0I4=I3+4
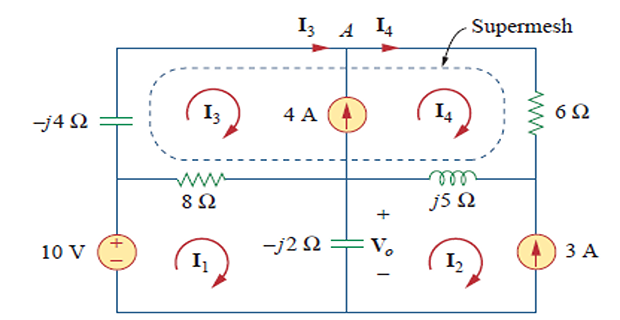
I1=3.618∠274.5∘AVo=−j2(I1−I2)=9.756∠222.32∘V