Natural Response of Series RLC Circuits
Demonstrative Video
Series RLC Circuit without Source
Second Order Circuits or RLC Circuits
First-order circuits containing only one energy storage element, combined with a passive network which partly determined the time taken by either the \(C\) or \(L\) to charge/discharge.
The D.E. resulted from analysis were always first-order.
A second-order circuit may have two storage elements of different type or the same type (provided elements of the same type cannot be represented by an equivalent single element).
The result is a second-order D.E. for any voltage or current of interest.
We will now need two initial conditions to solve each D.E.
Such circuits occur in a wide variety of applications, such as oscillators, filters, automobile suspension systems, temperature controllers, etc.

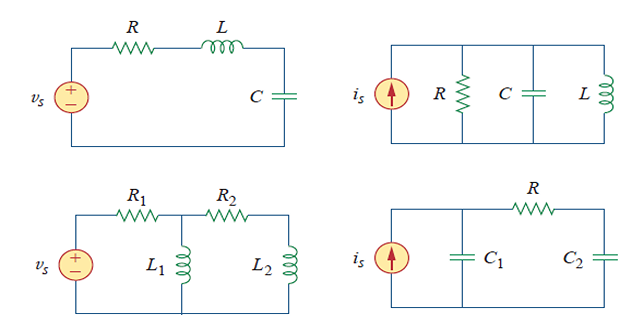

Finding Initial and Final Values
Unless otherwise stated \(v\) denotes capacitor voltage and \(i\) the inductor current
\(v(0), i(0), \dfrac{dv(0)}{dt}, \dfrac{di(0)}{dt}, i(\infty), v(\infty)\)
Note: carefully handle polarity of \(v(t)\) across the capacitor and \(i(t)\) through the inductor as per passive sign convention.
Remember capacitor voltage and inductor current are continuous \[v(0^+) = v(0^-) \quad \text{and} \quad i(0^+) = i(0^-)\] assuming switching has taken place at \(t=0\)
Solved Problem
The switch has been closed for a long time and open at \(t=0\). Find: (a) \(i\left(0^{+}\right), v\left(0^{+}\right)\),
(b) \(d i\left(0^{+}\right) / d t, d
v\left(0^{+}\right) / d t\), (c) \(i(\infty), v(\infty)\).

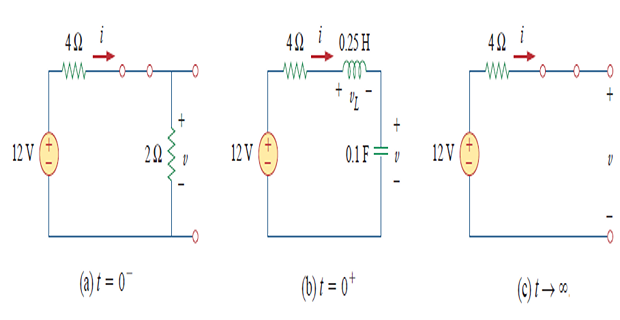 \[\begin{aligned}
&i\left(0^{-}\right)=\frac{12}{4+2}=2 \mathrm{~A}, \quad
v\left(0^{-}\right)=2 i\left(0^{-}\right)=4 \mathrm{~V} \\
&i\left(0^{+}\right)=i\left(0^{-}\right)=2 \mathrm{~A}, \quad
v\left(0^{+}\right)=v\left(0^{-}\right)=4 \mathrm{~V} \\
&i_{C}\left(0^{+}\right)=i\left(0^{+}\right)=2 \mathrm{~A}
\\
&\frac{d v\left(0^{+}\right)}{d
t}=\frac{i_{C}\left(0^{+}\right)}{C}=\frac{2}{0.1}=20 \mathrm{~V} /
\mathrm{s}
\end{aligned}\]
\[\begin{aligned}
&i\left(0^{-}\right)=\frac{12}{4+2}=2 \mathrm{~A}, \quad
v\left(0^{-}\right)=2 i\left(0^{-}\right)=4 \mathrm{~V} \\
&i\left(0^{+}\right)=i\left(0^{-}\right)=2 \mathrm{~A}, \quad
v\left(0^{+}\right)=v\left(0^{-}\right)=4 \mathrm{~V} \\
&i_{C}\left(0^{+}\right)=i\left(0^{+}\right)=2 \mathrm{~A}
\\
&\frac{d v\left(0^{+}\right)}{d
t}=\frac{i_{C}\left(0^{+}\right)}{C}=\frac{2}{0.1}=20 \mathrm{~V} /
\mathrm{s}
\end{aligned}\]
\[\begin{aligned} &-12+4 i\left(0^{+}\right)+v_{L}\left(0^{+}\right)+v\left(0^{+}\right)=0 \\ &\Rightarrow v_{L}\left(0^{+}\right)=12-8-4=0 \\ &\frac{d i\left(0^{+}\right)}{d t}=\frac{v_{L}\left(0^{+}\right)}{L}=\frac{0}{0.25}=0 \mathrm{~A} / \mathrm{s} \\ &i(\infty)=0 \mathrm{~A}, \quad v(\infty)=12 \mathrm{~V} \end{aligned}\]
The Source-Free Series RLC Circuit
\[\begin{aligned}
v(0) &=\frac{1}{C} \int_{-\infty}^{0} i d t=V_{0} \\
i(0) &=I_{0}
\end{aligned}\]
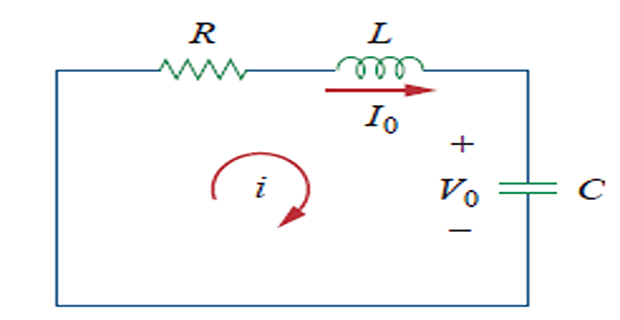
Applying KVL and then differentiating \[\begin{aligned} &R i+L \frac{d i}{d t}+\frac{1}{C} \int_{-\infty}^{t} i d t=0 \\ &\frac{d^{2} i}{d t^{2}}+\frac{R}{L} \frac{d i}{d t}+\frac{i}{L C}=0 \quad \Leftarrow \color{red}{\text{second-order D.E.}} \end{aligned}\]
Solution has general form \(i = A \cdot e^{st}\)
More initial condition \[\begin{aligned} &R i(0)+L \frac{d i(0)}{d t}+V_{0}=0 \\ & \Rightarrow \frac{d i(0)}{d t}=-\frac{1}{L}\left(R I_{0}+V_{0}\right) \end{aligned}\]
Substituting \(i = A \cdot e^{st}\) in second-order D.E. \[\begin{aligned} &\frac{d^{2} i}{d t^{2}}+\frac{R}{L} \frac{d i}{d t}+\frac{i}{L C}=0 \\ &\Rightarrow A s^{2} e^{s t}+\frac{A R}{L} s e^{s t}+\frac{A}{L C} e^{s t}=0 \\ & \Rightarrow A e^{s t}\left(s^{2}+\frac{R}{L} s+\frac{1}{L C}\right)=0 \end{aligned}\]
Since \(i=A e^{s t}\) is the assumed solution we are trying to find, only the expression in parentheses can be zero: \[s^{2}+\frac{R}{L} s+\frac{1}{L C}=0 \Leftarrow \color{red}{\text{characteristic equation of D.E.}}\]
Roots of the characteristic equation \[\begin{aligned} &s_{1}=-\frac{R}{2 L}+\sqrt{\left(\frac{R}{2 L}\right)^{2}-\frac{1}{L C}} \\ &s_{2}=-\frac{R}{2 L}-\sqrt{\left(\frac{R}{2 L}\right)^{2}-\frac{1}{L C}} \end{aligned}\]
Compact form \[\begin{aligned} &\boxed{s_{1}, s_{2}=-\alpha\pm\sqrt{\alpha^{2}-\omega_{0}^{2}}} \quad \boxed{\alpha=\frac{R}{2 L}} \quad \boxed{\omega_{0}=\frac{1}{\sqrt{L C}}} \end{aligned}\]
\(s_{1}\) and \(s_{2}\) : natural frequencies, in nepers per second \((\mathrm{Np} / \mathrm{s})\), because they are associated with the natural response of the circuit
\(\omega_{0}\) : resonant frequency or undamped natural frequency, in radians per second \((\mathrm{rad} / \mathrm{s})\)
\(\alpha\) : neper frequency or damping factor, in nepers per second.
In terms of \(\alpha\) and \(\omega_{0}\) Eq. can be written as \[s^{2}+\frac{R}{L} s+\frac{1}{L C}=0 \Rightarrow \boxed{s^{2}+2 \alpha s+\omega_{0}^{2}=0}\]
Natural response of the series RLC circuit \[i(t) = A_1\cdot e^{s_1t} + A_2\cdot e^{s_2t}\]
Constants \({A_1,A_2}\) are determined using initial values \(i(0)\) and \(\dfrac{di(0)}{dt}\)
Three types of solutions:
If \(\alpha>\omega_{0} \Rightarrow\) over-damped case
If \(\alpha=\omega_{0} \Rightarrow\) critically damped case
If \(\alpha<\omega_{0} \Rightarrow\) under-damped case
Over-damped Case:
\[\begin{aligned} &\boxed{s_{1}, s_{2}=-\alpha\pm\sqrt{\alpha^{2}-\omega_{0}^{2}}} \quad \boxed{\alpha=\frac{R}{2 L}} \quad \boxed{\omega_{0}=\frac{1}{\sqrt{L C}}} \end{aligned}\]
\(\alpha > \omega_0 \Rightarrow C > 4L/R^2\)
both roots \(s_1\) and \(s_2\) are negative and real
Response : \[i(t) = A_1\cdot e^{s_1t} + A_2\cdot e^{s_2t}\]
As \(t \uparrow\) response decays and approaches zero.
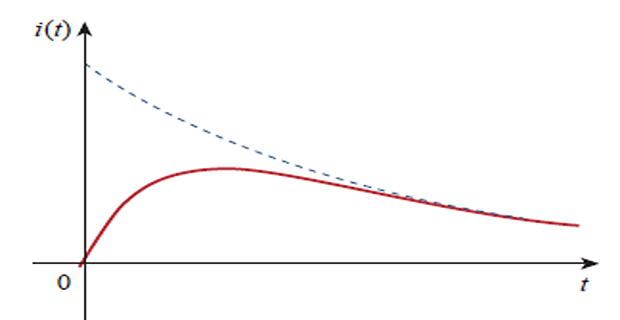
Critically Damped Case: \[\begin{aligned} &\boxed{s_{1}, s_{2}=-\alpha\pm\sqrt{\alpha^{2}-\omega_{0}^{2}}} \quad \boxed{\alpha=\frac{R}{2 L}} \quad \boxed{\omega_{0}=\frac{1}{\sqrt{L C}}} \end{aligned}\]
\(\alpha = \omega_0 \Rightarrow C = 4L/R^2\)
Roots : \[s_1 = s_2 = -\alpha = -\dfrac{R}{2L}\]
Response : \[i(t) = A_1\cdot e^{-\alpha t} + A_2\cdot e^{-\alpha t} = A_3 \cdot e^{-\alpha t} \quad (A_3 = A_1 + A_2)\]
Wrong solution, because the two initial conditions cannot be satisfied with the single constant \(A_3\) .
What then could be wrong?
When \(\alpha = \omega_0 = R/2L\)
\[ \begin{aligned} \frac{d^{2} i}{d t^{2}}+2 \alpha \frac{d i}{d t}+\alpha^{2} i &=0 \\ \frac{d}{d t}\left(\frac{d i}{d t}+\alpha i\right)+\alpha\left(\frac{d i}{d t}+\alpha i\right) &=0 \\ \frac{d f}{d t}+\alpha f &=0 \quad \left(f=\frac{d i}{d t}+\alpha i \right) \\ \frac{d i}{d t}+\alpha i &=A_{1} e^{-\alpha t} \quad \Leftarrow (\text{solution of}~ f)\\ e^{\alpha t} \frac{d i}{d t}+e^{\alpha t} \alpha i &=A_{1} \\ \frac{d}{d t}\left(e^{\alpha t} i\right) &=A_{1} \\ e^{\alpha t} i &=A_{1} t+A_{2} \Leftarrow \text{on Integrating}\\ i=&\left(A_{1} t+A_{2}\right) e^{-\alpha t} \end{aligned} \]
\[\boxed{ i=\left(A_{1} t+A_{2}\right) e^{-\alpha t}}\]
Reaches a maximum value at \(t=1/\alpha\), one time constant and then decays to zero

Under-damped case: \(\alpha < \omega_{0}\)
\[\begin{aligned} s_{1} &=-\alpha+\sqrt{-\left(\omega_{0}^{2}-\alpha^{2}\right)}=-\alpha+j \omega_{d} \\ s_{2} &=-\alpha-\sqrt{-\left(\omega_{0}^{2}-\alpha^{2}\right)}=-\alpha-j \omega_{d} \\ \omega_{d} &=\sqrt{\omega_{0}^{2}-\alpha^{2}} \end{aligned}\]
Response: \[\begin{aligned} i(t) &=A_{1} e^{-\left(\alpha-j \omega_{d}\right) t}+A_{2} e^{-\left(\alpha+j \omega_{d}\right) t} \\ &=e^{-\alpha t}\left(A_{1} e^{j \omega_{d} t}+A_{2} e^{-j \omega_{d} t}\right) \end{aligned}\]
Using Euler’s identities, \[e^{j \theta}=\cos \theta+j \sin \theta, \quad e^{-j \theta}=\cos \theta-j \sin \theta\]
we get \[\begin{aligned} i(t) &=e^{-\alpha t}\left[A_{1}\left(\cos \omega_{d} t+j \sin \omega_{d} t\right)+A_{2}\left(\cos \omega_{d} t-j \sin \omega_{d} t\right)\right] \\ &=e^{-\alpha t}\left[\left(A_{1}+A_{2}\right) \cos \omega_{d} t+j\left(A_{1}-A_{2}\right) \sin \omega_{d} t\right] \end{aligned}\]
Replacing constants \(\left(A_{1}+A_{2}\right)\) and \(j\left(A_{1}-A_{2}\right)\) with \(B_{1}\) and \(B_{2}\), \[i(t)=e^{-\alpha t}\left(B_{1} \cos \omega_{d} t+B_{2} \sin \omega_{d} t\right)\]
Presence of sine and cosine functions makes the natural response is exponentially damped and oscillatory in nature
Response has time constant of \(1/\alpha\) and period \(T=2\pi/\omega_d\)

Peculiar properties of an RLC network
The behaviour is due to damping - gradual loss of initial stored energy represented by decrease in response amplitude
Damping effect is due to \(R\) and damping factor \(\alpha\) determine the rate of damping
For lossless circuit \(R=0~\Rightarrow \alpha =0\), means \(LC\) circuit with \(\omega_0 = 1/\sqrt{LC}\)
\(\alpha < \omega_0~\Rightarrow\) response undamped and oscillatory
Adjusting \(R~\Rightarrow\) undamped, overdamped, critically-damped, or under-damped
Due to two types of storage elements oscillatory response is possible with flow of energy back and forth between the two
Ringing: The damped oscillation ehibited by underdamped response
Critically damped (decays fastest) is the borderline between underdamped and over-damped
Over-damped has longest settling time i.e. to dissipate the intial stored energy
Critically response is the best choice to led the response settle fastest without oscillation and ringing
Solved Problem
Find \(i(t)\) assuming the circuit has reached steady-state at \(t=0^{-}\)
For \(t<0~\Rightarrow\) switch closed \(\Rightarrow\) \(C \rightarrow\) OC and \(L \rightarrow\) SC
At \(t=0\) \[\begin{aligned} i(0)& = \dfrac{10}{4+6}=1~A\\ v(0)&=6i(0)=6~V \end{aligned}\]
For \(t>0~\Rightarrow\) source-free series RLC circuit \[\begin{aligned} \alpha & = \dfrac{R}{2L} = 9 \quad \omega_0 = \dfrac{1}{\sqrt{LC}}=10\\ s_{1,2} & = -\alpha \pm \sqrt{\alpha^2-\omega_0^2}= -9 \pm j4.359 \end{aligned}\]
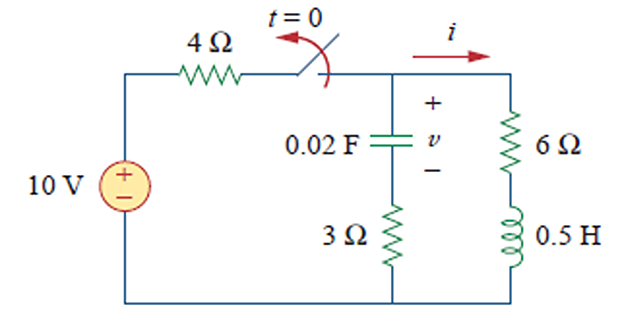

\[\begin{aligned} s_{1,2}&=-9 \pm j 4.359 ~\Rightarrow \alpha < \omega ~\Rightarrow \text{Under-damped} \\ i(t)&=e^{-9 t}\left(A_{1} \cos 4.359 t+A_{2} \sin 4.359 t\right) \\ i(0)&=1=A_{1} \\ \left.\frac{d i}{d t}\right|_{t=0}&=-\frac{1}{L}[R i(0)+v(0)]=-2[9(1)-6]=-6 \mathrm{~A} / \mathrm{s} \\ \frac{d i}{d t}&=-9 e^{-9 t}\left(A_{1} \cos 4.359 t+A_{2} \sin 4.359 t\right) \\ &+e^{-9 t}(4.359)\left(-A_{1} \sin 4.359 t+A_{2} \cos 4.359 t\right) \\ -6&=-9\left(A_{1}+0\right)+4.359\left(-0+A_{2}\right) \\ \Rightarrow \quad A_{2}&=0.6882 \\ i(t)&=e^{-9 t}(\cos 4.359 t+0.6882 \sin 4.359 t) \mathrm{A} \end{aligned}\]