Maximum Power Transfer Theorem
Demonstrative Video
Maximum Power Transfer
In applications such as communications it is desirable to maximize the power delivered to a load.
We will address the problem of delivering the maximum power to a load when given a system with known internal losses.
It should be noted that this will result in significant internal losses greater than or equal to the power delivered to the load.
The Thevenin equivalent is useful in finding the maximum power a linear circuit can deliver to a load assuming that \(R_L\) is adjustable.
\[p=i^{2} R_{L}=\left(\frac{V_{\mathrm{Th}}}{R_{\mathrm{Th}}+R_{L}}\right)^{2} R_{L}\]
\(V_{TH}\) and \(R_{TH}\) are fixed
Varying \(R_L\), power can be varied
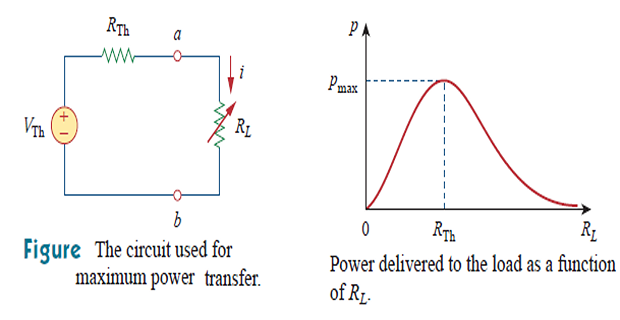
\(P\) is small for small or large values of \(R_L\)
\(P_{max}\) for some value of \(R_L\) between \(0\) to \(\infty\)
\(P_{max}\) is transferred to the load when \(R_L = R_{Th}\) as seen from the load
To prove differentiate \(P\) w.r.t \(R_L\) and equate to zero \[\begin{aligned} p=i^{2} R_{L}&=\left(\frac{V_{\mathrm{Th}}}{R_{\mathrm{Th}}+R_{L}}\right)^{2} R_{L}\\ \frac{d p}{d R_{L}} &=V_{\mathrm{Th}}^{2}\left[\frac{\left(R_{\mathrm{Th}}+R_{L}\right)^{2}-2 R_{L}\left(R_{\mathrm{Th}}+R_{L}\right)}{\left(R_{\mathrm{Th}}+R_{L}\right)^{4}}\right] \\ &=V_{\mathrm{Th}}^{2}\left[\frac{\left(R_{\mathrm{Th}}+R_{L}-2 R_{L}\right)}{\left(R_{\mathrm{Th}}+R_{L}\right)^{3}}\right]=0 \\ &= \left(R_{TH}-2R_{L}\right)=0 \\ & \Rightarrow \boxed{R_{L} = R_{Th}} \end{aligned}\]
The maximum power transferred \[\boxed{P_{max} = \dfrac{V_{Th}^2}{4R_{Th}}}\]
