Balanced Three-Phase Circuits
Demonstrative Video
Introduction
A single-phase ac power system consists of a generator connected through a pair of wires (a transmission line) to a load.
An ac generator designed to develop a single sinusoidal voltage for each rotation of the shaft (rotor) is referred to as a single-phase ac generator.
If the number of coils on the rotor is increased in a specified manner, the result is a polyphase ac generator, which develops more than one ac phase voltage per rotation of the rotor.
Three-phase system most frequently used for power transmission.
Polyphase System
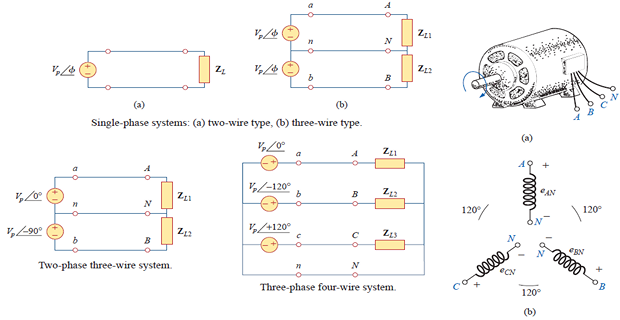
In the normal household system is a \(1-\phi\) three-wire system because the terminal voltages have the same magnitude and the same phase
Circuits or systems in which the ac sources operate at the same frequency but different phases are known as polyphase
Advantages of \(3-\phi\) System over \(1-\phi\) System
For same Electric power:
Generation (Alternator) : Power to weight ratio \(\uparrow\), size \(\downarrow\), overall cost \(\downarrow\), Weight \(\downarrow ~\Rightarrow\) transportation and installation become convenient and less space is required.
T & D : conductor material \(\downarrow ~\Rightarrow\) economical
Under UPF condition:
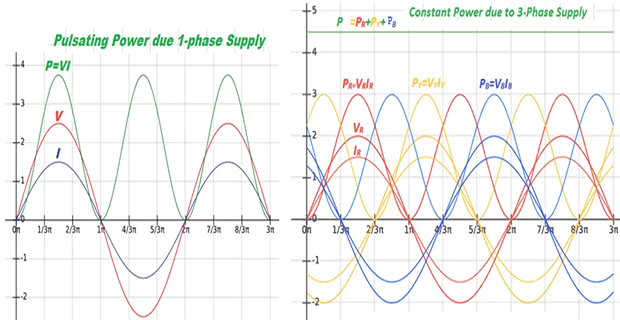
Same condition of Power to weight ratio for 3-\(\phi\) IM (Load) and TF.
3-\(\phi\) Induction Motor are self-starting but 1-\(\phi\) not so some arrangements are required which increase cost.
3-phase motor is having better power factor
Reliability under fault condition.
A \(3\phi\) system can feed a \(1\phi\) load, whereas vice-versa is not possible.
Balanced Three-Phase Voltages
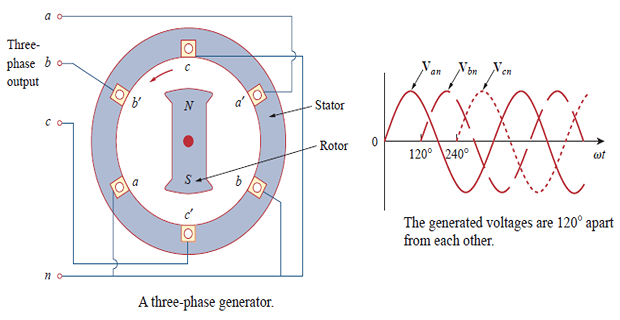
\(3-\phi\) voltages are produced by alternator having coils with terminals \(a-a^{\prime}\), \(b-b^{\prime}\), and \(c-c^{\prime}\) that are physically placed at \(120^{\circ}\) apart.
As the rotor rotates, its magnetic field cuts the flux from the three coils and then voltage is induced in the coils.
Induced voltages are equal in magnitude but out of phase by \(180^{\circ}\).
Balanced phase voltages are equal in magnitude and are out of phase with each other by \(120^{\circ}\)
A \(3\phi\) system \(\sim\) \(3 \times 1\phi\) circuits.
The voltage sources can be either Y-connected or delta-connected.
\(\mathbf{V_{an}}\), \(\mathbf{V_{bn}}\), \(\mathbf{V_{cn}}\) \(\Rightarrow\) Phase voltages
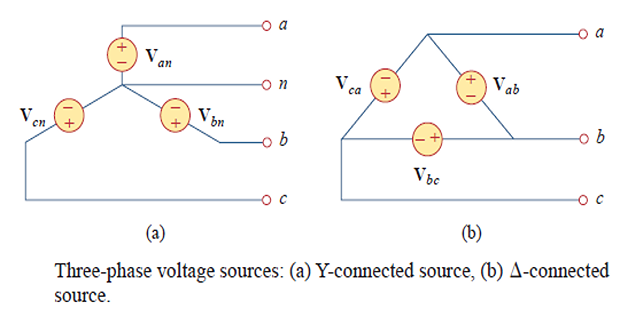
\[\begin{aligned} &\mathbf{V}_{a n}+\mathbf{V}_{b n}+\mathbf{V}_{c n}=0\\ &\left|\mathbf{V}_{a n}\right|=\left|\mathbf{V}_{b n}\right|=\left|\mathbf{V}_{c n}\right|\\ &\mathbf{V}_{a n}=V_{p} \angle 0^{\circ}\\ &\mathbf{V}_{b n}=V_{p} \angle -120^{\circ}\\ &\mathbf{V}_{c n}=V_{p} \angle-240^{\circ}=V_{p} \angle+120^{\circ} \end{aligned}\]
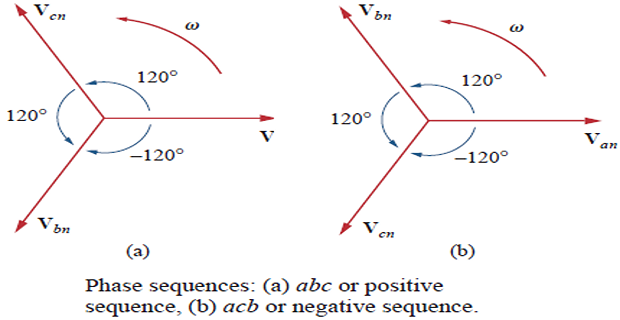
abc or positive sequence
produced when rotor rotates counter-clockwise
\[\begin{aligned}
&\mathbf{V}_{a n}=V_{p} \angle 0^{\circ}\\
&\mathbf{V}_{c n}=V_{p} \angle -120^{\circ}\\
&\mathbf{V}_{b n}=V_{p} \angle-240^{\circ}=V_{p}
\angle+120^{\circ}
\end{aligned}\]
acb or negative sequence
produced when rotor rotates clockwise
\[\begin{aligned} \mathbf{V}_{a n}+\mathbf{V}_{b n}+\mathbf{V}_{c n} &=V_{p} \angle 0^{\circ}+V_{p} \angle-120^{\circ}+V_{p} \angle+120^{\circ} \\ &=V_{p}(1.0-0.5-j 0.866-0.5+j 0.866) \\ &=0 \end{aligned}\]
The phase sequence is the time order in which the voltages pass through their respective maximum values.
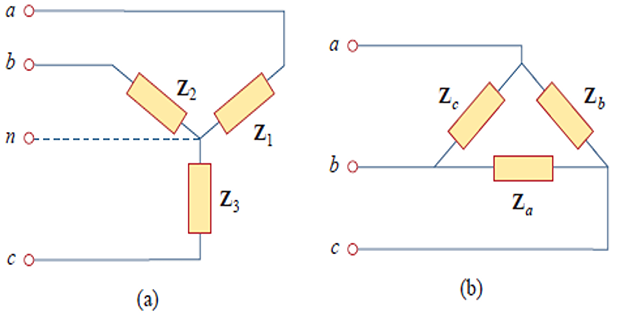
A balanced load is one in which the phase impedances are equal in magnitude and in phase.
For Balanced Loads: \[\begin{aligned} &\mathbf{Z}_{1}=\mathbf{Z}_{2}=\mathbf{Z}_{3}=\mathbf{Z}_{Y} \\ &\mathbf{Z}_{a}=\mathbf{Z}_{b}=\mathbf{Z}_{c}=\mathbf{Z}_{\Delta} \\ &\mathbf{Z}_{\Delta}=3 \mathbf{Z}_{Y} \quad \text { or } \quad \mathbf{Z}_{Y}=\frac{1}{3} \mathbf{Z}_{\Delta} \end{aligned}\]
Source-Load Combinations:
\(Y-Y\)
\(Y-\Delta\)
\(\Delta-Y\)
\(\Delta - \Delta\)
Problem
Determine the phase sequence of the set of voltages \[\begin{gathered} v_{a n}=200 \cos \left(\omega t+10^{\circ}\right) \\ v_{b n}=200 \cos \left(\omega t-230^{\circ}\right), \quad v_{c n}=200 \cos \left(\omega t-110^{\circ}\right) \end{gathered}\] Solution:
The voltages can be expressed in phasor form as \[\mathbf{V}_{a n}=200 \angle 10^{\circ} \mathrm{V}, \quad \mathbf{V}_{b n}=200 \angle-230^{\circ} \mathrm{V}, \quad \mathbf{V}_{c n}=200 \angle-110^{\circ} \mathrm{V}\]
We notice that \(\mathbf{V}_{a n}\) leads \(\mathbf{V}_{c n}\) by \(120^{\circ}\) and \(\mathbf{V}_{c n}\) in turn leads \(\mathbf{V}_{b n}\) by \(120^{\circ}\). Hence, we have an \(acb\) sequence.