Step Response of RC Circuits
Demonstrative Video
RC Circuit with Source
Step Response of an RC Circuit
When dc source (voltage or current) is suddenly applied to an RC circuit , the source can be modelled as a step function, and the response is known as a step response.
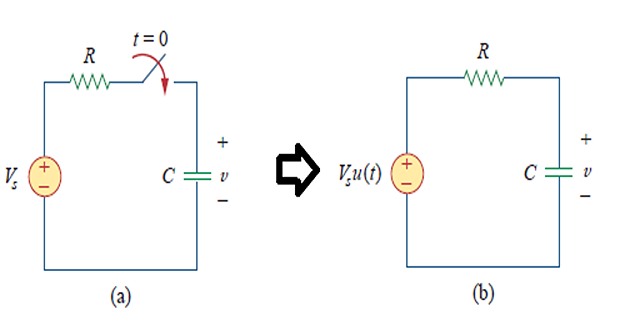
Since the voltage of a capacitor cannot change instantaneously, \[v(0^-)=v(0^+) = V_0\]
Applying KCL, \[C \frac{d v}{d t}+\frac{v-V_{s} u(t)}{R}=0 \quad \Rightarrow~ \frac{d v}{d t}+\frac{v}{R C}=\frac{V_{s}}{R C} u(t)\] where, \(v\) is the voltage at \(t>0\)
\[\begin{gathered} \frac{d v}{d t}+\frac{v}{R C}=\frac{V_{s}}{R C} u(t) \\ \frac{d v}{d t}+\frac{v}{R C}=\frac{V_{s}}{R C} \\ \frac{d v}{d t}=-\frac{v-V_{s}}{R C} \\ \frac{d v}{v-V_{s}}=-\frac{d t}{R C} \end{gathered}\] \[\begin{gathered} \frac{d v}{v-V_{s}}=-\frac{d t}{R C} \\ \left.\ln \left(v-V_{s}\right)\right|_{V_{0}} ^{v(t)}=-\left.\frac{t}{R C}\right|_{0} ^{t} \\ \ln \left(v(t)-V_{s}\right)-\ln \left(V_{0}-V_{s}\right)=-\frac{t}{R C}+0 \\ \ln \frac{v-V_{s}}{V_{0}-V_{s}}=-\frac{t}{R C} \\ \frac{v-V_{s}}{V_{0}-V_{s}}=e^{-t / \tau}, \quad \tau=R C \\ v-V_{s}=\left(V_{0}-V_{s}\right) e^{-t / \tau} \\ v(t)=V_{s}+\left(V_{0}-V_{s}\right) e^{-t / \tau}, \quad t>0 \end{gathered}\]
Complete or Total Response of an RC Circuit
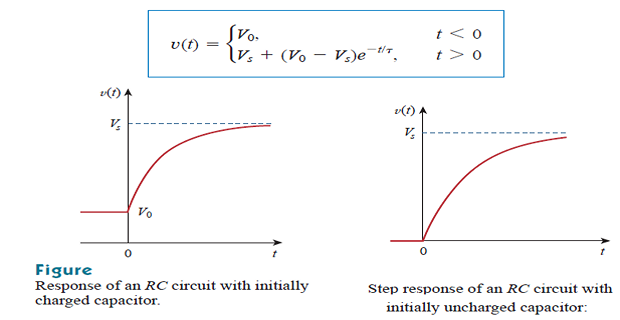
\[\begin{aligned}
&v(t)= \begin{cases}0, & t<0 \\
V_{s}\left(1-e^{-t / \tau}\right), & t>0\end{cases} \\
&v(t)=V_{s}\left(1-e^{-t / \tau}\right) u(t) \\
&i(t)=C \frac{d v}{d t}=\frac{C}{\tau} V_{s} e^{-t / \tau},
\quad \tau=R C, \quad t>0 \\
&i(t)=\frac{V_{s}}{R} e^{-t / \tau} u(t)
\end{aligned}\]
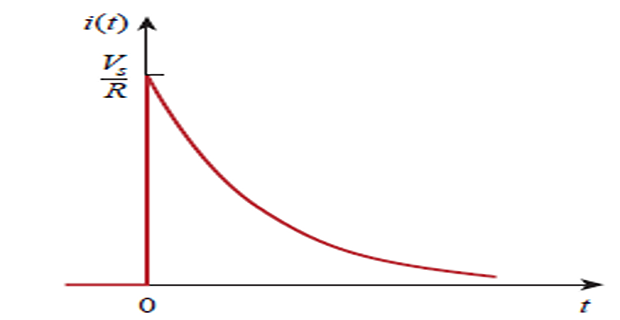
\[\begin{aligned} \text { Complete response }&=\underset{\text { stored energy }}{\text { natural response }}+\underset{\text { independent source }}{\text { forced response }}\\ v = v_n+v_f & \quad v_n = V_0\cdot e^{-t/\tau} \quad v_f = V_s(1-e^{-t/\tau})\\ \text { Complete response }&=\underset{\text { transient }}{\text { temporary part }}+\underset{\text { steady-state }}{\text { permanent part }}\\ v = v_t+v_{ss} & \quad v_t = (V_0-V_s)e^{-t/\tau} \quad v_{ss} = V_s \end{aligned}\]
Transient response is the circuit’s temporary response that will die out with time.
Steady-state response is the behaviour of the circuit a long time after an external excitation is applied.
Problem Solving Steps
\[v(t) = v(\infty) + [v(0)-v(\infty)]e^{-t/\tau}\]
Determine the initial capacitor voltage \(v(0)\)
Determine the final capacitor voltage \(v(\infty)\)
Determine the time-constant \(\tau\)
Note : if the switch changes position at time \(t=t_{0}\) instead of at \(t=0\), there is a time delay in the response so equation becomes, \[v(t)=v(\infty)+\left[v\left(t_{0}\right)-v(\infty)\right] e^{-\left(t-t_{0}\right) / \tau}\]
Solved Problem
The switch has been in position \(A\) for a long time. At \(t=0\), the switch moves to \(B\). Determine \(v(t)\) for \(t>0\) and calculate its value at \(t=1 \mathrm{~s}\) and \(4 \mathrm{~s}\).
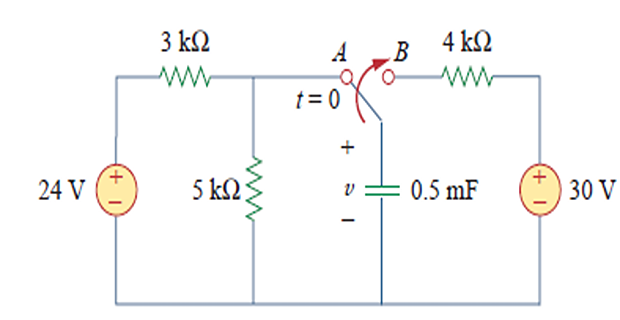
\[\begin{gathered} v\left(0^{-}\right)=\frac{5}{5+3}(24)=15 \mathrm{~V} \\ v(0)=v\left(0^{-}\right)=v\left(0^{+}\right)=15 \mathrm{~V} \\ \tau=R_{\mathrm{Th}} C=4 \times 10^{3} \times 0.5 \times 10^{-3}=2 \mathrm{~s} \\ v(t)=v(\infty)+[v(0)-v(\infty)] e^{-t / \tau} \\ =30+(15-30) e^{-t / 2}=\left(30-15 e^{-0.5 t}\right) \mathrm{V} \\ \text { At } t=1, \quad v(1)=30-15 e^{-0.5}=20.9 \mathrm{~V}\\ \text { At } t=4, \quad v(4)=30-15 e^{-2}=27.97 \mathrm{~V} \end{gathered}\]