Kirchhoff's Laws in AC Circuits
Demonstrative Video
Kirchhoff’s Laws in the Frequency Domain
KVL: \[\begin{aligned} &v_{1}+v_{2}+\cdots+v_{n}=0 \\ \Rightarrow &V_{m 1} \cos \left(\omega t+\theta_{1}\right)+V_{m 2} \cos \left(\omega t+\theta_{2}\right)+\cdots+V_{m n} \cos \left(\omega t+\theta_{n}\right)=0 \\ \Rightarrow &\operatorname{Re}\left(V_{m 1} e^{j \theta_{1}} e^{j \omega t}\right)+\operatorname{Re}\left(V_{m 2} e^{j \theta_{2}} e^{j \omega t}\right)+\cdots+\operatorname{Re}\left(V_{m n} e^{j \theta_{n}} e^{j \omega t}\right)=0 \\ \Rightarrow &\operatorname{Re}\left[\left(V_{m 1} e^{j \theta_{1}}+V_{m 2} e^{j \theta_{2}}+\cdots+V_{m n} e^{j \theta_{n}}\right) e^{j \omega t}\right]=0 \\ \Rightarrow &\operatorname{Re}\left[\left(\mathbf{V}_{1}+\mathbf{V}_{2}+\cdots+\mathbf{V}_{n}\right) e^{j \omega t}\right]=0 \\ \Rightarrow &\mathbf{V}_{1}+\mathbf{V}_{2}+\cdots+\mathbf{V}_{n}=0 \quad \text { Since } e^{j \omega t} \neq 0 \end{aligned}\]
KCL: \[\begin{aligned} &i_{1}+i_{2}+\cdots+i_{n}=0 \\ &\mathbf{I}_{1}+\mathbf{I}_{2}+\cdots+\mathbf{I}_{n}=0 \end{aligned}\]
Impedance Combinations
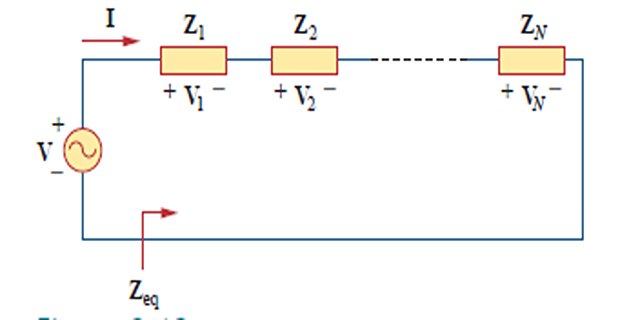
In Series:
\[\begin{aligned} &\mathbf{V}=\mathbf{V}_{1}+\mathbf{V}_{2}+\cdots+\mathbf{V}_{N}\\ &=\mathbf{I}\left(\mathbf{Z}_{1}+\mathbf{Z}_{2}+\cdots+\mathbf{Z}_{N}\right) \\ &\mathbf{Z}_{\mathrm{eq}}=\frac{\mathbf{V}}{\mathbf{I}}=\mathbf{Z}_{1}+\mathbf{Z}_{2}+\cdots+\mathbf{Z}_{N} \end{aligned}\]
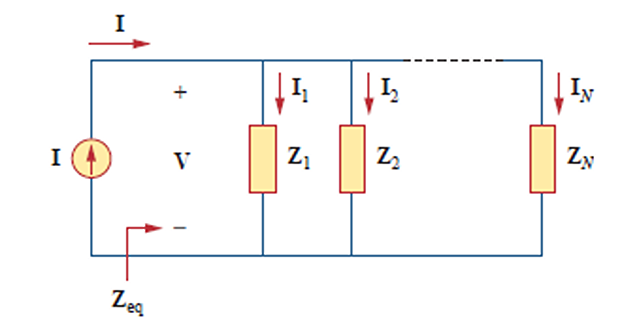
In Parallel:
\[\begin{aligned} &\mathbf{I}=\mathbf{I}_{1}+\mathbf{I}_{2}+\cdots+\mathbf{I}_{N}\\ &=\mathbf{V}\left(\frac{1}{\mathbf{Z}_{1}}+\frac{1}{\mathbf{Z}_{2}}+\cdots+\frac{1}{\mathbf{Z}_{N}}\right) \\ &\frac{1}{\mathbf{Z}_{\mathrm{eq}}}=\frac{\mathbf{I}}{\mathbf{V}}=\frac{1}{\mathbf{Z}_{1}}+\frac{1}{\mathbf{Z}_{2}}+\cdots+\frac{1}{\mathbf{Z}_{N}} \end{aligned}\]
Voltage division & Current division
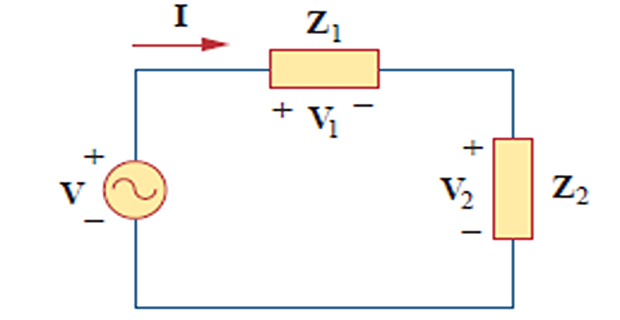
Voltage division:
\[\begin{aligned}
&\mathbf{V}_{1}=\frac{\mathbf{Z}_{1}}{\mathbf{Z}_{1}+\mathbf{Z}_{2}}
\mathbf{V}\\ &
\mathbf{V}_{2}=\frac{\mathbf{Z}_{2}}{\mathbf{Z}_{1}+\mathbf{Z}_{2}}
\mathbf{V}
\end{aligned}\]
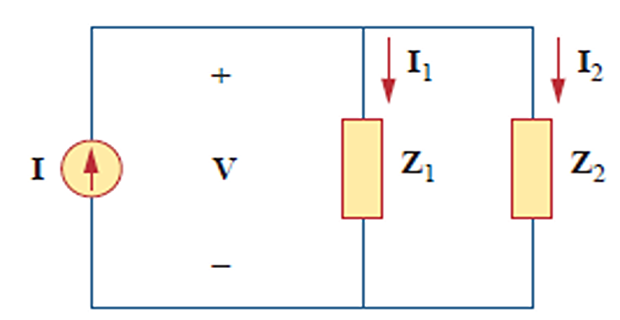
Current division
\[\begin{aligned}
&
\mathbf{I}_{1}=\frac{\mathbf{Z}_{2}}{\mathbf{Z}_{1}+\mathbf{Z}_{2}}
\mathbf{I} \\
&
\mathbf{I}_{2}=\frac{\mathbf{Z}_{1}}{\mathbf{Z}_{1}+\mathbf{Z}_{2}}
\mathbf{I}
\end{aligned}\]
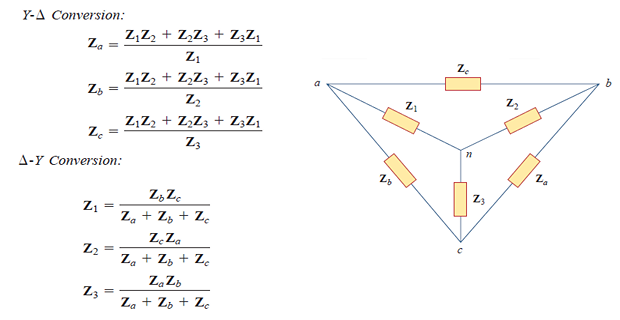
STAR-DELTA Transformation
Problem
Find the input impedance for the circuit operating at \(\omega = 50\) rad/sec.
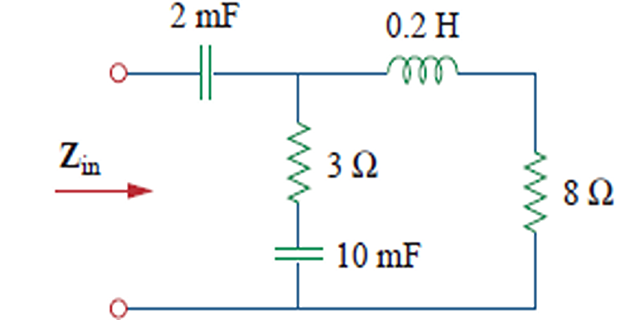
\[\begin{gathered} \mathbf{Z}_{1}=\frac{1}{j \omega C}=\frac{1}{j 50 \times 2 \times 10^{-3}}=-j 10 \Omega \\ \mathbf{Z}_{2}=3+\frac{1}{j \omega C}=3+\frac{1}{j 50 \times 10 \times 10^{-3}}=(3-j 2) \Omega \\ \mathbf{Z}_{3}=8+j \omega L=8+j 50 \times 0.2=(8+j 10) \Omega \\ \mathbf{Z}_{\text {in }}=\mathbf{Z}_{1}+\mathbf{Z}_{2} \| \mathbf{Z}_{3}=-j 10+\frac{(3-j 2)(8+j 10)}{11+j 8} \\ =-j 10+\frac{(44+j 14)(11-j 8)}{11^{2}+8^{2}}=-j 10+3.22-j 1.07 \Omega \\ \mathbf{Z}_{\text {in }}=3.22-j 11.07 \Omega \end{gathered}\]